Linformer: Self-Attention with Linear Complexity

URL

https://arxiv.org/pdf/2006.04768.pdf

TL;DR

• 本方法—— Linformer 使用矩阵的低秩来降低原始 Transformer 的 Multi-HEAD Attention 计算的时空复杂度
• 不同 Transformer 结构的复杂度
  

Algorithm

原始 Transformer 使用的 Multi-HEAD Attention

$head_i = Attention(QW_i^Q,KW_i^K,VW_i^V)=softmax[\frac{QW_i^Q(KW_i^K)^T}{\sqrt d_k}]VW_i^V$
其中： $K,Q,V \in \mathbb R^{n\times d_m} \ \ \ W_i^Q,W_i^K\in \mathbb R^{d_m\times d_k}$
所以： $softmax[\frac{QW_i^Q(KW_i^K)^T}{\sqrt d_k}] \in \mathbb {R} ^{n\times n}$ ，n 表示序列长度，所以原始 Transformer 使用的 Multi-HEAD Attention 的时空复杂度为 $O(n^2)$

Linformer 对 Multi-HEAD Attention 的修改

• 将 $KW_i^K, VW_i^V\in \mathbb R^{n\times d_k}$ 投影到 $E_iKW_i^K, F_iVW_i^V\in \mathbb R^{k\times d_k}$ ，其中 k 是一个常数，时空复杂度变成了 $O(n)$ ，其中，E、F 都是可学习的投影矩阵， $E,F \in \mathbb R^{k\times n}$
• $\bar{head_i} = Attention(QW_i^Q,E_iKW_i^K, F_iVW_i^V)=softmax[\frac{QW_i^Q(E_iKW_i^K)^T}{\sqrt d_k}]F_iVW_i^V$
• 投影矩阵 E、F 可共享参数，分为：
  • Headwise sharing： $E_i=E,\ \ F_i=F, \ \ for\ each\ layer$
  • Key-value sharing： $E_i=E = F_i, \ \ for\ each\ layer$
  • Layerwise sharing： $E, F, \ \ layer\ sharing$

理论依据与结果

• 特征值的长尾分布
  
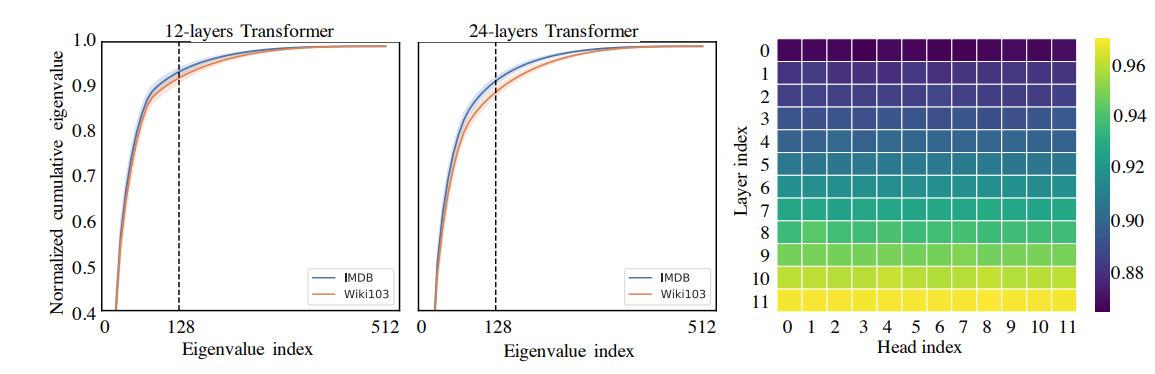
• 效果（与 BERT-base 对比）
  

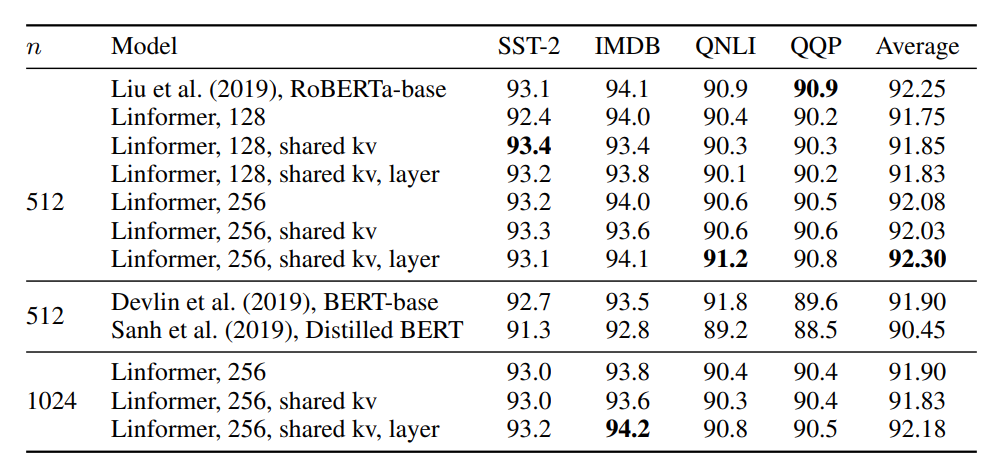
Thoughts

• 文中提到不使用奇异值分解来得到低秩矩阵的原因是：奇异值分解会引入额外的计算量，并且无法共享参数
• 代码被打包为了 linformer 的 pip 包，可以在 torch 框架下直接使用