AdderNet: Do We Really Need Multiplications in Deep Learning?

Paper Reading Note

URL

https://arxiv.org/pdf/1912.13200.pdf

TL;DR

1. 使用-L1距离代替了Conv

2. 因为-L1距离永远<=0，所以还是保留了bn，另外在梯度回传的时候加了HardTanh

3. 实际训练很慢，收敛需要的epoch很多

Algorithm

模式匹配方式

• 卷积本质上是一种模式匹配方式，但是模式匹配方式不是只有卷积，L1距离同样可以衡量模式的相似程度

• L1距离只使用加法，理论速度比卷积快

卷积的数学表达（输入h*w*c）

• $Y(m, n, t) = \sum_{i=0}^d\sum_{j=0}^d\sum_{k=0}^{c_{in}} S(X(m+i,n+j,k) , F(i,j,k,t))$

  其中: $S(x, y) = x \times y$

-L1距离的数学表达

• $Y(m, n, t) = -\sum_{i=0}^d\sum_{j=0}d\sum_{k=0}^{c_{in}} |X(m+i,n+j,k) - F(i,j,k,t) | $

求导

• 卷积是乘法和加法，乘法是交换门，也就是说输出对卷积核的梯度可以表示为：

  • $\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)} = X(m+i,n+j,k)$

  • $\frac{\partial Y(m,n,t)}{\partial X(m+i,n+j,k)} = F(i,j,k,t)$

• -L1距离求导，由于绝对值函数梯度是分段函数，所以:

  • $ \frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)} = sng(X(m+i,n+j,k) - F(i,j,k,t))$

  • $ \frac{\partial Y(m,n,t)}{\partial X(m+i,n+j,k)} = sng(F(i,j,k,t) - X(m+i,n+j,k))$

  其中: $sng(x) = \left\{\begin{matrix} -1, & x < 0\\ 0, & x = 0\\ 1, & x > 0 \end{matrix}\right.$

优化

• 分段函数求导麻烦，所以输出对卷积核的梯度，直接去掉符号函数，

  $ \frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)} = X(m+i,n+j,k) - F(i,j,k,t)$ ，简单粗暴

• 对于输出对feature的导数，论文中没有直接去掉符号函数，而是将符号函数换成了HardTanh函数，这个函数用在梯度上的时候还有一个大家熟悉的名字——梯度截断

  $HardTanh(x) = \left\{\begin{matrix} 1, & x > 1\\ x, & -1 < x < 1\\ -1, & x < -1 \end{matrix}\right.$

  $x$ 表示梯度

• 自此：反向传播时用到的梯度已经变形为：

  $ \frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)} = X(m+i,n+j,k) - F(i,j,k,t)$

  $ \frac{\partial Y(m,n,t)}{\partial X(m+i,n+j,k)} = HardTanh(F(i,j,k,t) - X(m+i,n+j,k))$

• 学习率：论文中详细的讲解了这个自适应学习率是如何推导出来的，如果想了解建议去看原文，这里直接说结论：

  $\alpha_l = \frac{\eta \sqrt K}{||\Delta(F_l)||_2}$

  (论文第二版中这个 $\sqrt K$ 在分母位置，看了源码，还是以第三版为准)

  其中， $K$ 表示卷积核滤波器中元素的个数， $||...||_2$ 表示矩阵的F范数

优化部分一堆公式不够直观，直接上源码

class adder(Function):
    @staticmethod
    def forward(ctx, W_col, X_col):
        ctx.save_for_backward(W_col, X_col)
        # -L1距离，其中x_col是使用img2col处理过的
        output = -(W_col.unsqueeze(2) - X_col.unsqueeze(0)).abs().sum(1)
        return output

    @staticmethod
    def backward(ctx, grad_output):
        W_col, X_col = ctx.saved_tensors
        # 对卷积核的梯度，直接去掉了符号函数sgn
        grad_W_col = (
            (X_col.unsqueeze(0) - W_col.unsqueeze(2)) * grad_output.unsqueeze(1)
        ).sum(2)
        # 这里是乘上推导出的自适应学习率，\eta=0.2
        grad_W_col = (
            grad_W_col
            / grad_W_col.norm(p=2).clamp(min=1e-12)
            * math.sqrt(W_col.size(1) * W_col.size(0))
            / 5
        )
        # 梯度截断，也就是所谓的HardTanh
        grad_X_col = (
            -(X_col.unsqueeze(0) - W_col.unsqueeze(2)).clamp(-1, 1)
            * grad_output.unsqueeze(1)
        ).sum(0)

        return grad_W_col, grad_X_col

实际运行

• 真的慢，可能是由于img2col还有求L1距离都是在python中做的，所以训练速度真的好慢啊!

• 真的难收敛，官方源码中，使用resnet20（conv -> L1）训练CIFAR10，设置的默认epoch次数为400，训练CIFAR10都需要400 epoch…

• 真的不稳定，不像传统Conv网络随着训练次数，网络准确率逐步提高，或者在极小范围内抖动，AdderNet训练过程中，epoch 23结束后在val上准确率可能55%，第epoch 24结束后，val上的准确率直接到了28%，而且不是因为学习率太大导致的，抖动范围真的大…

• 最终结果：AdderNet-ResNet20 在 CIFAR-10 上 epoch-400 最高正确率：91.67%

Thoughts

• 虽然这个网络目前问题还很多，而且作者的理论很糙，有些地方简单粗暴，但是这也许是神经网络加速的一种思路

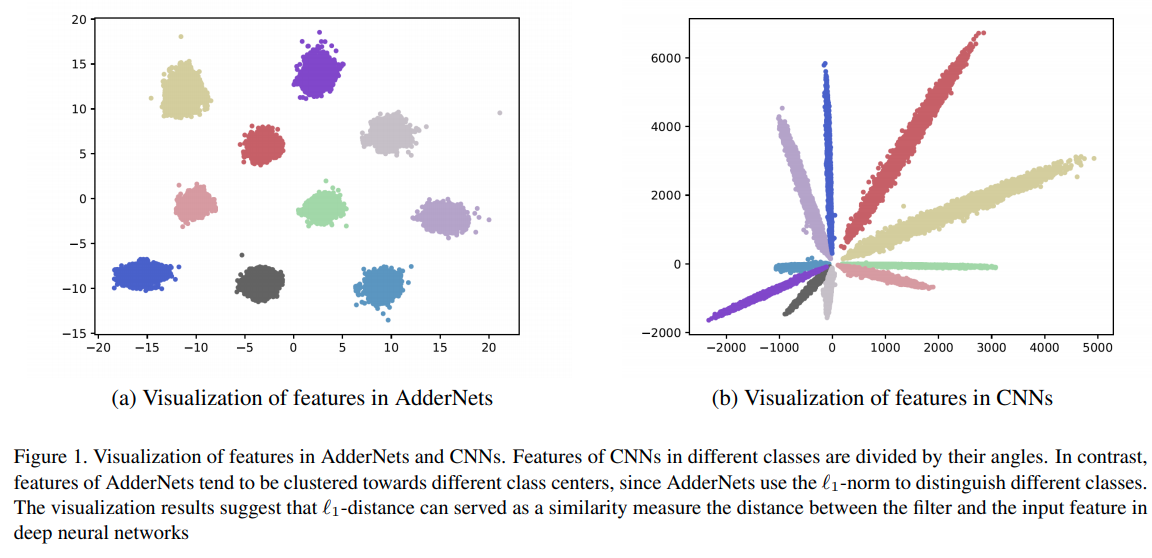
与CNN的对比