DO-Conv: Depthwise Over-parameterized Convolutional Layer

URL

https://arxiv.org/pdf/2006.12030.pdf

TL;DR

• 传统过参数化网络，在训练阶段能提高收敛速度并提高算法表现，但在推理阶段速度会变慢

• 本文提出一种过参数化卷积 DO-Conv，在训练阶段有过参数化的优点——收敛速度快、算法表现好，在推理阶段将 DO-Conv 转化为标准卷积，不会带来任何额外耗时

• DO-Conv 实际上是在训练阶段，将标准卷积拆分成标准卷积和Depthwise卷积的叠加；在推理阶段之前，将拆分后的标准卷积和Depthwise卷积再合并为一个标准卷积

Algorithm

何为过参数化？

• 过参数化可以理解为：通过使用更多的参数，增大模型的假设空间，增加模型的表达能力（线性与非线性），从而加速训练甚至提高算法表现

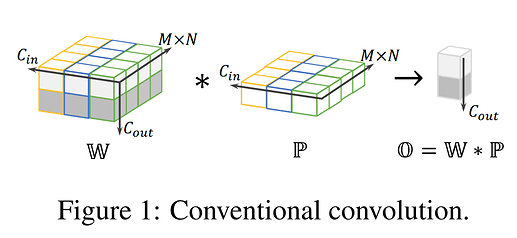
标准卷积与Depthwise卷积的数学表示：

• $O = W \times P$

  • $W \in \mathbb{R}^{C_{out} \times (M \times N) \times C_{in}}$ ，表示 kernels，每一个 $kernel.shape == (C_{in}, M, N)$ ，一共 $C_{out}$ 个 kernel

  • $P \in \mathbb{R}^{(M \times N) \times C_{in}}$ ，表示输入 feature map 被 kernel 覆盖的 patch，每一个 $patch.shape == (C_{in}, M, N)$

  • $O \in \mathbb{R}^{C_{out}}$ ，表示卷积结果

  

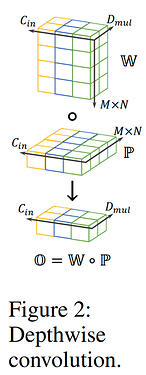
Depthwise 卷积的数学表示：

• $O = W \circ P$

  • $W \in \mathbb{R}^{(M \times N) \times D_{mul} \times C_{in}}$ ，表示 kernels，每一个 $kernel.shape == ( M, N)$ ，每组（每个通道为一组） $D_{mul}$ 个 kernel，一共 $C_{in}$ 组

  • $P \in \mathbb{R}^{(M \times N) \times C_{in}}$ ，表示输入 feature map 被 kernel 覆盖（所有通道）的 patch，每一个 $patch.shape == (C_{in}, M, N)$

  • $O \in \mathbb{R}^{D_{mul} \times C_{in}}$ ，表示卷积结果

    

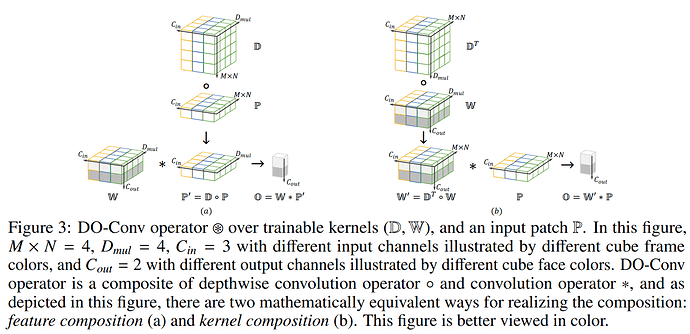
DO-Conv 的数学表示：

• $O = (D, W) \star P$

• feature composition： $O = W \times (D \circ P)$

• kernel composition： $O = (D^T \circ W ) \times P$

  • $W \in \mathbb{R}^{C_{out}\times D_{mul}\times C_{in}}$ ，表示 kernels_w，每一个 $kernel_w.shape ==\text{ ( }C_{in}, D_{mul})$ ，一共$C_{out}$ 个 kernel_w

  • $D \in \mathbb{R}^{(M\times N)\times D_{mul}\times C_{in}}$ ，表示 kernels_d，每一个 $kernel_d.shape == ( M, N)$ ，每组（每个通道为一组） $D_{mul}$ 个 kernel_d，一共 $C_{in}$ 组

  • $P \in \mathbb{R}^{(M\times N)\times C_{in}}$ ，表示输入 feature map 被 kernel 覆盖（所有通道）的 patch，每一个 $patch.shape == (C_{in}, M, N)$

  • $O \in \mathbb{R}^{C_{out}}$ ，表示卷积结果

这与Depthwise Separable 卷积有什么区别？

• 相同点：

  • feature composition 可以看做是先对 feature map 做 Depthwise Conv ，再做标准卷积

• 区别：

  • Depthwise Separable Conv 是`DO-Conv $D_{mul} = 1$ 的特殊情况

DO-Conv 怎么能保证参数量比标准卷积多呢？

• 标准卷积卷积核：

  • $W_1 \in \mathbb{R}^{C_{out}\times (M\times N)\times C_{in}}$

• DO-Conv 卷积核：

  • $W_2 \in \mathbb{R}^{C_{out}\times D_{mul}\times C_{in}}$

  • $D \in \mathbb{R}^{(M\times N)\times D_{mul}\times C_{in}}$

• 当 $D_{mul} = (M \times N)$ 时， $W2 = W1$ ，此时 $ D + W_2 > W_1$ ，DO-Conv 拥有更多的参数量

• 所以规定： $D_{mul} \ge (M \times N)$

怎么能保证推理阶段不增加耗时呢？

• 训练阶段 W 和 D 都是可优化参数，所以模型会保存 W 和 D

• 推理阶段之前，使用 kernel composition 对 W 和 D 处理， $W' = D^T \circ W$ ，然后就使用 $W'$ 去做标准卷积， $W'.shape == W_1.shape$ ，所以 inference 阶段不会增加任何耗时

DO-Conv 分组卷积 / Depthwise卷积

• $O = (D, W) \odot P$

• feature composition： $O = W \circ (D \circ P)$

• kernel composition： $O = (D^T \circ W^T )^T \circ P$

Thoughts

• 设 a = a1 * a2，能不能从数学角度证明学习 a1 * a2 比直接学习 a 更容易，效果更好？

• 芯片上常常不支持 1 * 1 Conv，能否将输入的 $(N^2 \times C_{in}, H, W)$ 使用 PixelShuffle 运算 reshape 成为 $(C_{in}, N \times H, N \times W)$ ，再使用 $kernel.shape == (C_{in},N, N), stride = N$ 的标准卷积去算？

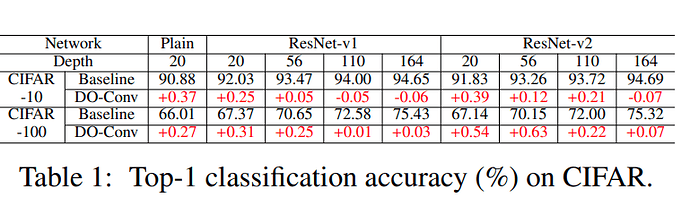
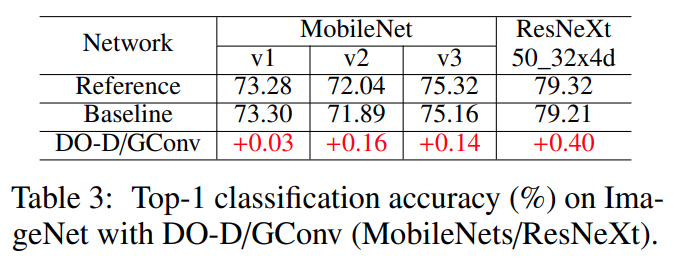
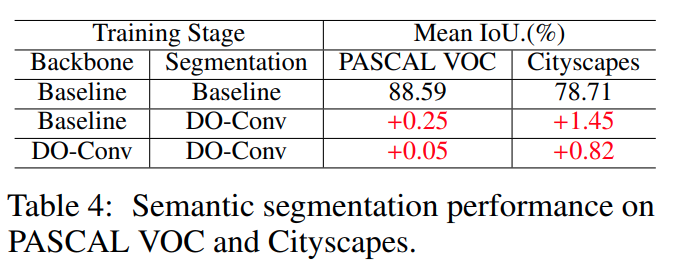
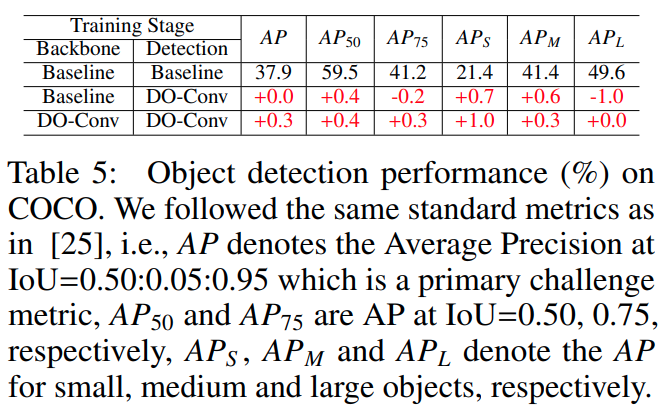
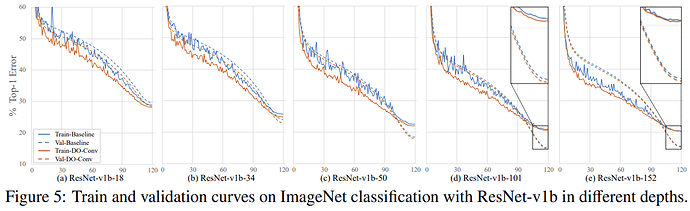
DO-Conv 网络的实际表现

• 在所有用到卷积的地方，无脑替换为 DO-Conv 基本都能涨点