Deep Learning with Low Precision by Half-wave Gaussian Quantization

URL

https://openaccess.thecvf.com/content_cvpr_2017/papers/Cai_Deep_Learning_With_CVPR_2017_paper.pdf

TL;DR

• 量化网络的反向传播通常使用STE，造成前后向结果与梯度不匹配，所以通常掉点严重
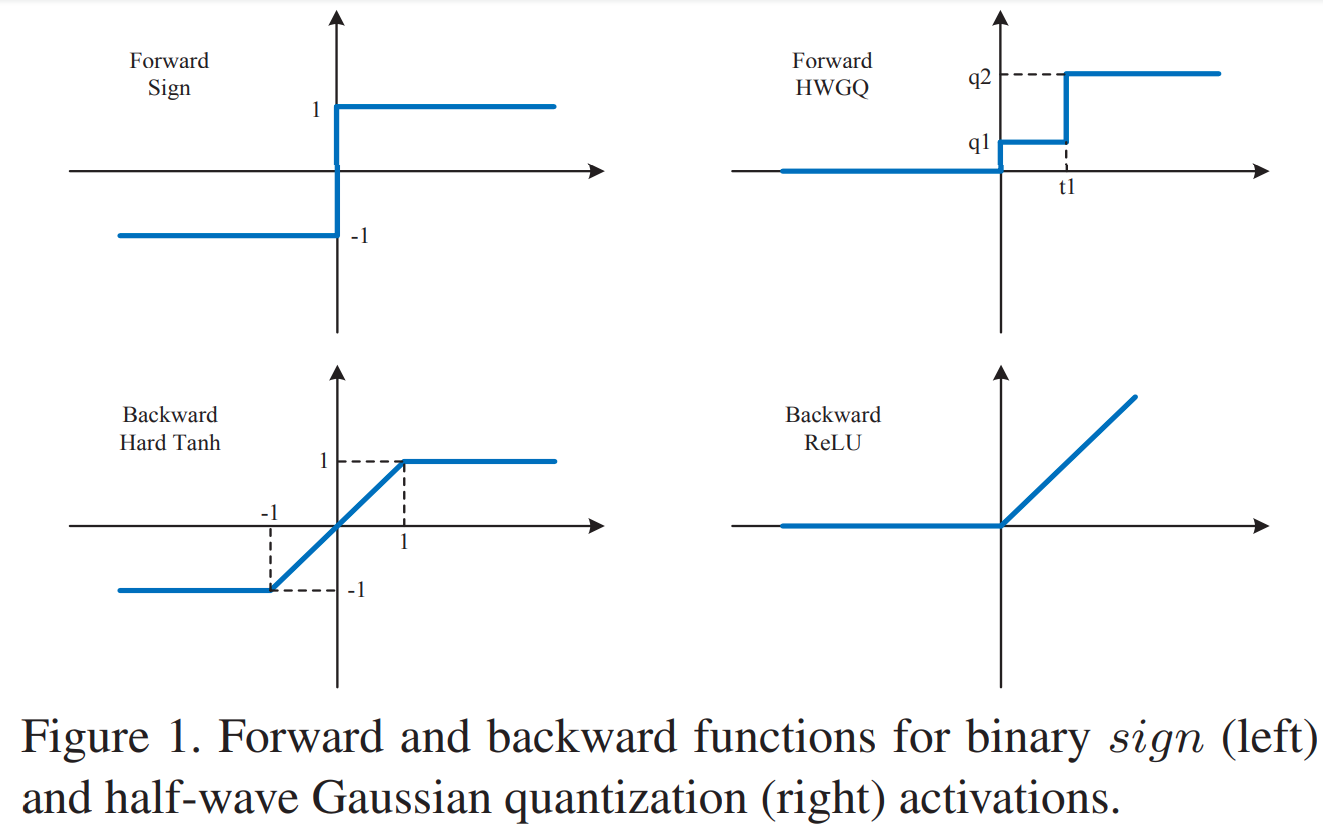
• 前向过程中：HWGQ网络使用半波高斯分布量化函数Q代替sign函数
• 反向过程中：HWGQ网络使用ReLU及其变体代替HardTanh来近似前向量化过程的梯度

Algorithm

• weight binarization
  $I \times W \approx \alpha (I \oplus B)$
  其中， $B$ 表示二值化权重， $I$ 表示输入， $\alpha \in \mathbb{R^+}$ 表示缩放系数， $\oplus$ 表示无系数卷积
• 常用 activations 量化
  • 常用二值化特征量化函数：sign(x) = 1 if x >=0 else -1
  • 常用二值量化函数的梯度：hardTanh(x) = 1 if abs(x) <= 1 else 0
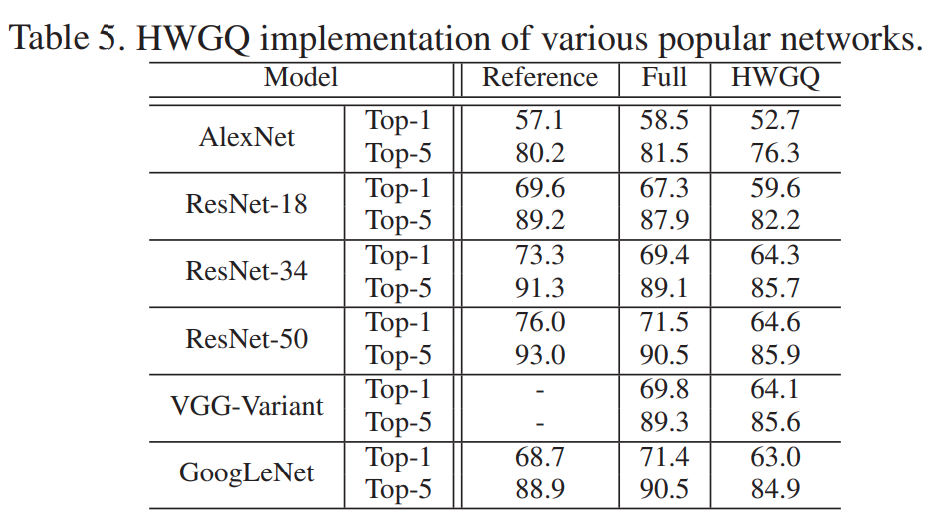
• HWGQ activations 量化
  • 前向过程：
    $Q(x) = \begin{cases} q_i, \ \ \ \ if\ \ x\in (t_i, t_{i+1}] \\ 0, \ \ \ \ \ if \ \ x\le 0 \end{cases}$
    $q_{i+1} - q_i = \Delta,\ \ \ \ \forall i$
    当 $\Delta$ 为一个常数的时候， $q_i$ 为均匀分布，但 $t_i$ 不是均匀分布
    其中超参数 $Q^{\star}(x) = arg\min_Q E_x[(Q(x) - x)^2] = arg\min_Q \int p(x) (Q(x) - x)^2 dx$，其中 $p(x)$ 表示半波高斯分布的概率密度
    • 看了源码发现：
      • 当 f_bits=2 时， $q = \{0.538, 1.076, 1.614\},\ \ \ t=\{-\infty, 0.807, 1.345, +\infty\}$
      • 当 f_bits=1 时， $q = {0.453, 1.51},\ \ \ t={-\infty, 0.97, +\infty} $
  • 反向过程：

    • 反向过程有三种方式，分别为：

      • ReLU
        $\tilde Q(x) = \begin{cases}1,\ \ \ \ if\ \ x > 0\\0,\ \ \ \ otherwise \end{cases}$
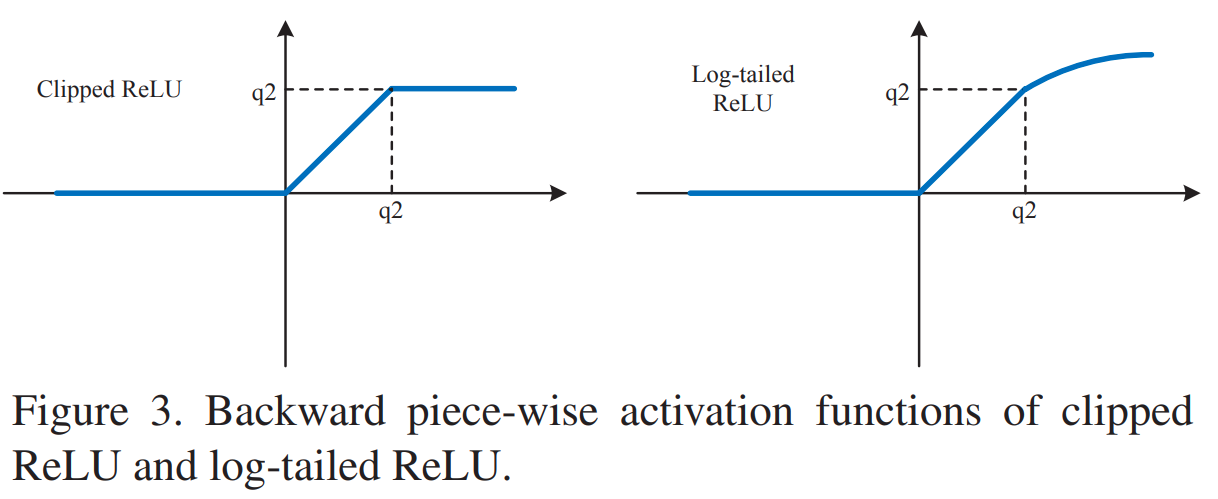
      • Clipped ReLU
        $\tilde Q(x) = \begin{cases}q_m,\ \ \ \ x>q_m\\1,\ \ \ \ \ if\ \ x \in (0, q_m]\\0,\ \ \ \ \ otherwise \end{cases}$
        源码中，f_bits=2时， $q_m = 1.614$ ，f_bits=1时， $q_m = 1.515$
      • Log-tailed ReLU
        $\tilde Q(x) = \begin{cases}\frac{1}{x-\tau},\ \ \ \ x>q_m\\1,\ \ \ \ \ if\ \ x \in (0, q_m]\\0,\ \ \ \ \ otherwise \end{cases}$

    • 实际发现Clipped ReLU效果最好，复杂度低

Thoughts

• 算法想法很本质，目的是减小STE带来的前向与反向的不一致
• 没与DoReFa-Net的效果对比，当比特数较多的时候，round()与使用半波高斯近似那个更好？

图表