URL
https://arxiv.org/pdf/2007.06191.pdf
TL;DR
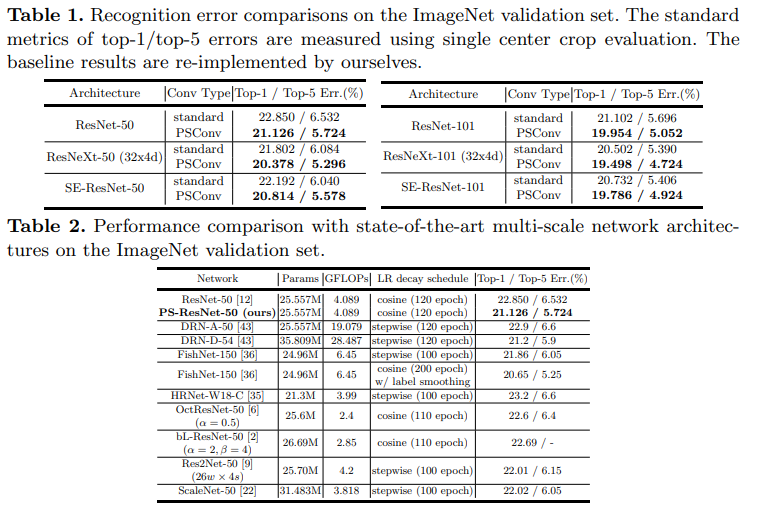
- 本文提出了一种新颖的卷积方式——PSConv,参数量与计算量都不变的情况下可以提高网络特征提取能力
- PSConv的本质是一种dilated系数周期性变化的空洞卷积,周期性变化发生在 Cin 和 Cout 两个“正交”坐标系中
Algorithm
什么是PSConv
- 标准卷积:
Hc,x,y=∑k=1Cin∑i=−2K−12K−1∑j=−2K−12K−1Gc,k,i,jFk,x+i,y+j
其中,F表示输入feature, F∈RCin×H×W ,G表示kernel, G∈RCout×Cin×K×K ,H表示一个kernel卷积输出 H∈R1×H×W ,i,j分表表示kernel中的点距离kernel中心在H于W方向上的偏移
- 空洞卷积:
Hc,x,y=∑k=1Cin∑i=−2K−12K−1∑j=−2K−12K−1Gc,k,i,jFk,x+id,y+jd
其中:id表示 偏移 i * 空洞系数 d
- PSConv:
Hc,x,y=∑k=1Cin∑i=−2K−12K−1∑j=−2K−12K−1Gc,k,i,jFk,x+iD(c,k),y+jD(c,k)
其中:i * D(c, k)表示 偏移 i * 空洞系数 D(c, k),D是空洞系数矩阵,D∈RCout×Cin ,D(i, j) 表示 第 i 个 kernel 第 j channel 的空洞系数 d
空洞系数矩阵D设计的基本法
- D矩阵的一行表示一个kernel,kernel 的通道数为 Cin
- PSConv 是将这 Cin 通道分为 P 个周期,每个周期的长度为 t=⌈PCin⌉
- 每个周期 t 个空洞系数 d={d1,d2,...,dt} ,实验证明当 t=4,d={1,2,1,4} 效果最好
- 另外D矩阵的列上也要具有周期性,方法是让每一行相对与上一行偏移 1个相位(一个周期 t 个相位)
效果
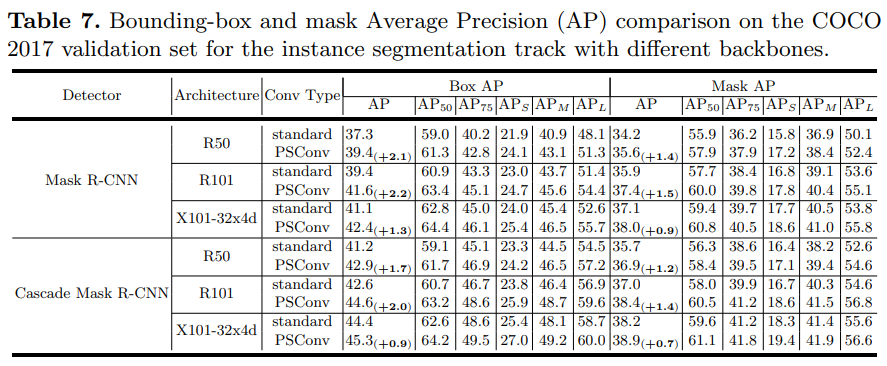
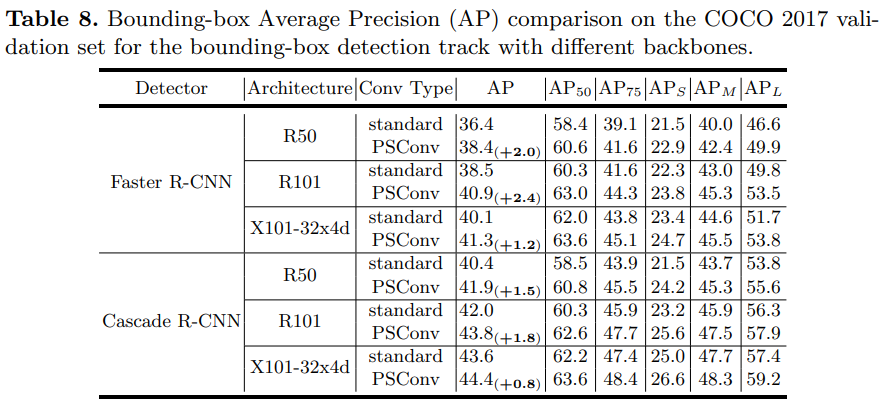
- 涨点,替换什么什么就涨点,原因是使用一种类似周期性金字塔kernel的方法,得到了非常有想象力的感受野
- 虽然不增加参数量与计算量,但是train与inference都会变慢,所以作者附录中给出了一种优化实现方式,是将每个周期的相同相位合并到一起使用group Conv,然后再shuffle index,与ShuffleNet一个意思
- 优化后确实会变快,可以将PS-ResNet-50/101在inference速度提升到与标准ResNet-50/101基本一致
- 消融实验对比了只在 Cin 或者 只在Cout 上周期性变化,发现哪个轴上周期变化都是必要的
- 当 t = 1时,D中只会包含一种元素,此时PSconv退化为标准空洞卷积
- PSConv 可以加入 group 参数,每个 group 内单独周期变化
Thoughts
- 不增加计算量和参数量,且文章附录中提出经过优化实现可以将PS-ResNet-50/101在inference速度提升到与标准ResNet-50/101基本一致。
- 如果在硬件设计中,预留了dilated Conv接口,并借鉴文中的优化实现方式,使用分组卷积+index shuffle减小filter通道间dilated不同的问题,这种白送的点也挺香的
图表
- 标准卷积与PSConv (可以带group参数)
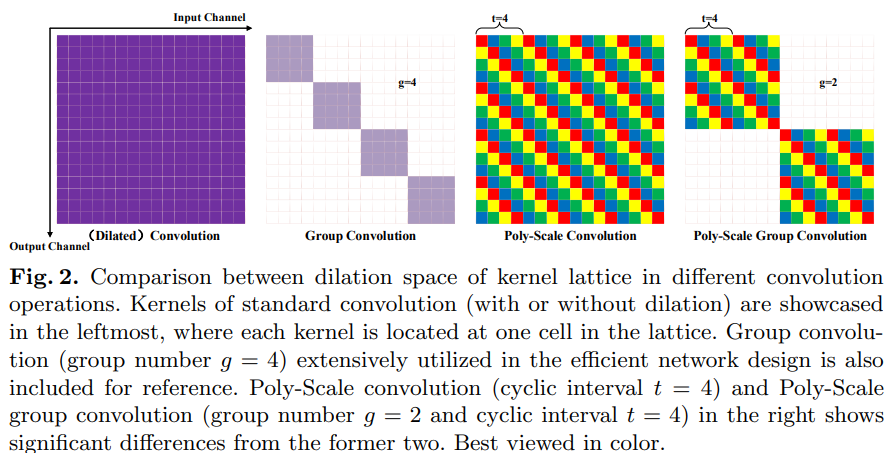
- PS group Conv
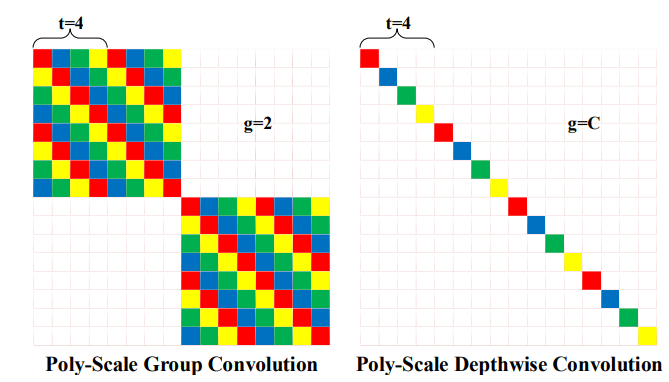
- 优化实现

- 搜索 t 与 d
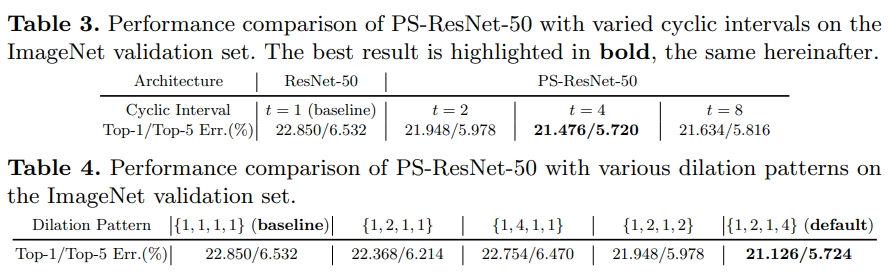
- 横纵坐标周期消融实验

- 涨点涨点涨点…