LS-Net: Learning to Solve Nonlinear Least Squares for Monocular Stereo

URL

https://arxiv.org/pdf/1809.02966.pdf

TL;DR

• 提出一种端到端的可训练的优化方法，通过近似 Hessian 优化方法，解决非线性最小二乘法问题

• 从训练数据中隐式的学习正则化与先验信息

• 第一个将可学习的优化器用于单目视觉光度误差估计任务中

Algorithm

背景知识

非线性最小二乘法求解

• 最小二乘法问题： $E = \frac{1}{2}\sum_{j} r_j^2(x),\ \ \ \ \ r_j(x)$ 表示 x 第 j 项的 L1 误差
• 常用方法： Gauss-Newton (GN)、Levenberg-Marquadt (LM)
• 求解过程：
  • 对误差进行一阶估计： $r(x_i+\Delta x_i)=r(x_i)+J_i\Delta x_i,\ \ \ J_i = \frac{dr}{dx}|_{x=x_i}$ ，J 是雅各比矩阵
  • 最优变化量： $\Delta x_i=\arg_{\Delta x_i}\min \frac{1}{2}||r_i+J_i\Delta x_i||^2$
  • GN 法获得最优变化量： $J_i^TJ_i\Delta x_i = - J_i^Tr_i$ ，如果 $J_i^TJ_i$ 可逆，则最优变化量 $\Delta x_i=-(J_i^TJ_i)^{-1}J_i^Tr_i$
  • LM 法获得最优变化量（在 GN 的基础上加入超参数—— 阻尼系数 $\lambda$）： $\Delta x_i=-(J_i^TJ_i + \lambda \ diag(J_i^TJ_i))^{-1}J_i^Tr_i$
  • 本方法：基于 GN 加入了更多的可学习参数，使用梯度下降优化

任务描述

• 输入一段图像序列，输出深度估计（depth）与姿态估计（pose），为了估计较大范围的深度，所以网络实际估计深度的倒数： $z = \frac{1}{d}$
• 所以本任务优化目标函数： $E(x) = \frac{1}{2}||r(x)||^2,\ \ \ x=(z, p)$

网络结构

网络结构包含 bootstrap network、iterative network、refinement network

• bootstrap network： 生成低分辨率（ $\frac{H}{4}, \frac{W}{4}$ ）的粗糙估计（一个简单的包含下采样的CNN）
• iterative network：重复迭代与细化，本文使用 LSTM （非线性最小二乘法优化也用于此处）
• refinement network：上采样（双线性插值法）

iterative network 优化过程

• 其中 $f_{\theta_0}$ 表示 bootstrap network， $f_{\theta}$ 表示 Convolutional LSTM Cell

• 由于 J 具体空间局部性，所以这里使用的 LSTM 是 Convolutional LSTM
• $\begin{bmatrix} \Delta x_i\\ h_{i+1} \end{bmatrix} = LSTM_{cell}(\Phi(J_i,r_i),h_i,x_i;\theta),\ \ \ x_{i+1} = x_i + \Delta x_i$ ，这里的 $x_i$ 并不是真的输入到 LSTM 中，如 Algorithm 1 所示， $x_i$ 用来产生 $J_i$ 从而产生 $\Phi(J_i, r_i)$
• 其中雅各比矩阵的变形 $\Phi(J_i,r_i) = [J^TJ,r]$
  • 理论上 $\Phi(J_i,r_i) = [(J^TJ)^{-1}J,r]$ ，但由于求逆会引入较大的计算量，并且不会产生额外的信息量，所以简化 $\Phi(J_i,r_i) = [J^TJ,r]$
  • 由于雅各比矩阵是稀疏的，所以使用了下图的方法对 $J^TJ$ 进行了压缩

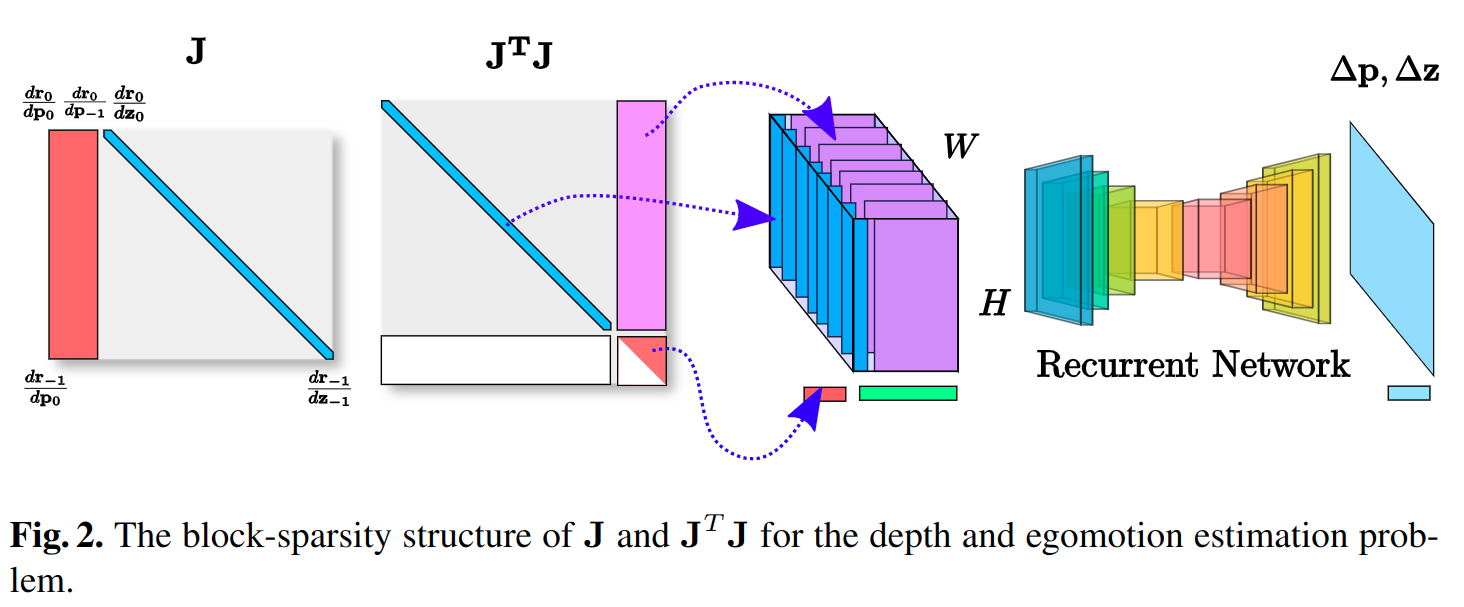
损失函数

• depth 与 pose 的 L1 误差的加权和

Thoughts

• 本文的创新点在于 Convolutional LSTM 中输入的不是 $x_i$ ，而是压缩后的二阶雅各比矩阵，用来拟合 $\Delta x_i$ ，可以通过近似 GN 法，产生超一阶优化的效果

• GN ： $\Delta x_i=-(J_i^TJ_i)^{-1}J_i^Tr_i$ ，本文： $\Delta x_i=LSTM(J_i^TJ_i,r_i)$ ，即把 $[(J_i^TJ_i)^{-1}J_i,r_i] --> [J_i^TJ_i,r_i]$ 并加入了 LSTM 梯度下降优化

• 本文的网络没有官方开源，也找不到民间实现，所以对网络的细节不是特别明白