Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts

URL

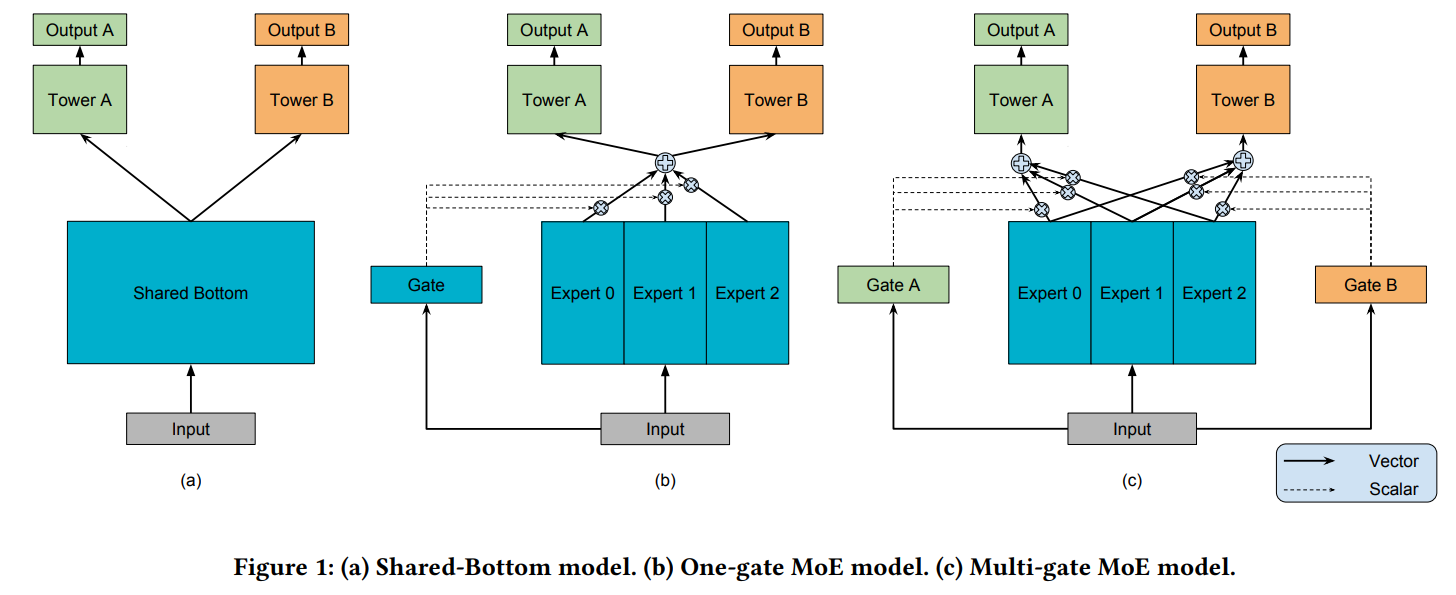
其中 A 和 B 分别表示两个任务，Tower 表示与任务相关的金字塔头部，Expert 表示专家 bottom network，Gate 表示任务相关的权重生成网络

上图 a 表示 Bottom Shared Architecture: 传统共享 bottom network 的多任务结构，共享 bottom network (Backbone) 进行特征提取，将提取到的特征分别送入任务相关头部，缺点是如果任务 A 和 B 之间的相关性较弱，那么共用一个 Backbone 是危险的
上图 b 表示 One-gate Mixture-of-Experts Architecture，有多个 Expert 做 Backbone 进行不同维度的特征提取，只有一个 Gate network 用于给每个任务生成 Expert 权重
上图 c 表示 Multi-gate Mixture-of-Experts Architecture，有多个 Expert 做 Backbone 进行不同维度的特征提取，每个任务有单独的 Gate network 生成唯一的 Expert 权重

Bottom Shared

$y_k = h^k(f(x))$

其中 $k$ 表示 任务数， $f()$ 表示 shared bottom， $h^k$ 表示 第 k 个任务的 Tower
OMOE

$y_k=h^k(\sum_{i=1}^n g(x)_i f_i(x))$ ， where $\sum_{i=1}^n g(x)_i=1,\ \ g(x) \in \mathbb R^n$

其中 $n$ 表示 专家数， $g$ 表示 Gate network（由于 $g(x)$ 要经过 Softmax，使得 logits -> prob，所以 $\sum_{i=1}^n g(x)_i=1$ ）
MMOE

$y_k=h^k(\sum_{i=1}^n g^k(x)_i f_i(x))$ ， where $\sum_{i=1}^n g^k(x)_i=1$

$g^k(x)=softmax(W_{gk}x)$ ，其中 $x \in \mathbb R^d,\ \ W_{gk} \in \mathbb R^{n\times d}, \ so \ \ g^k(x) \in \mathbb R^n$

与 OMOE 不同之处在于： 每个任务有单独的 Gate network，不共享

是有效的优化，针对任务相关性差的多任务场景，确实能有效涨点
本质是一种参数的堆砌，没看到很创新的点
除了堆参数之外，还有一个很致命的问题，每个 Gate 以及 Expert 都是独立的，实际实现过程中只能使用 for loop 依次计算，效率很低，速度很慢