URL
https://arxiv.org/pdf/2109.09310.pdf
TL;DR
- 本文提出一种多功能的卷积核,可以有效提高算法效果,降低计算量与存储空间
- 具体做法是:将 一个 主卷积核与 多个 二值 mask 点积生成 多个次级卷积核,用次级卷积核进行计算
- 二值 mask 包括 H、W、C 方向,即每个次级卷积核的 H、W、C 都可能不同
Algorithm
思路
- 神经网络轻量化(参数量与计算量)常用方法:
- 模型压缩,主要包括:
- 网络结构轻量化,主要包括:
- Xception
- MobileNet series
- ShuffleNet series
- OctConv
- MixConv
- 本论文思路:
- 将 一个 主卷积核与 多个 二值 mask 点积生成 多个次级卷积核
- 二值 mask 作用在 H、W、C 上,所以每 个次级卷积核的感受野可能不同,关注的 channel 可能不同
网络设计
在空间方向设计多功能卷积
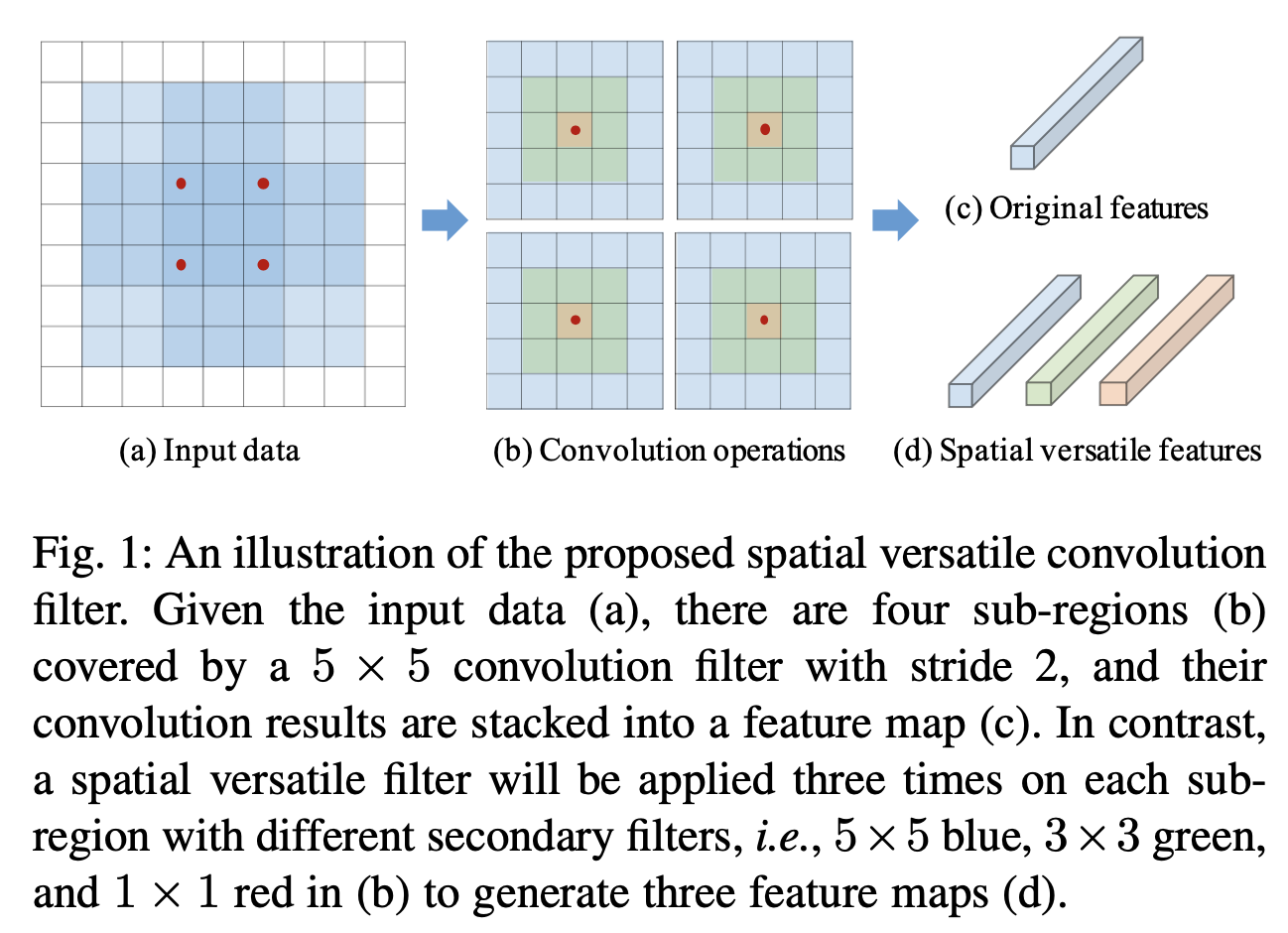
-
空间方向就是指 H、W 方向
-
图中用一个极端例子演示,实际上二值 mask 不是由人手工设计的,而是神经网络自动学习得到
-
普通卷积计算过程:
- input: x∈RH×W×c
- filter: f∈Rd×d×c
- output: y=f@x , y∈RH′×W′ (“@” means convolution operation)
-
多功能卷积计算过程(在空间方向上):
- filter: f∈Rd×d
- binery mask: Mi(p,q,c)={1, if p,q≥i∣p,q≤d+1−i0, otherwise
- secondary filter: {f^1, f^2, ... ,f^s} , s=⌈2d⌉ , f^i=Mi∘f
- output: y=[(Mi∘f) @ x+b1,... ,(Ms∘f) @ x+bs],
s.t. s=⌈2d⌈, {Mi}i=1s∈{0, 1}d×d×c
“[]” means concat,bi means bias
- naive version:output: y=∑i=1s(Mi∘f) @ x+b=[∑i=1s(Mi)∘f] @ x+b,
s.t. s=⌈2d⌈, {Mi}i=1s∈{0, 1}d×d×c
在 Channel 方向设计多功能卷积
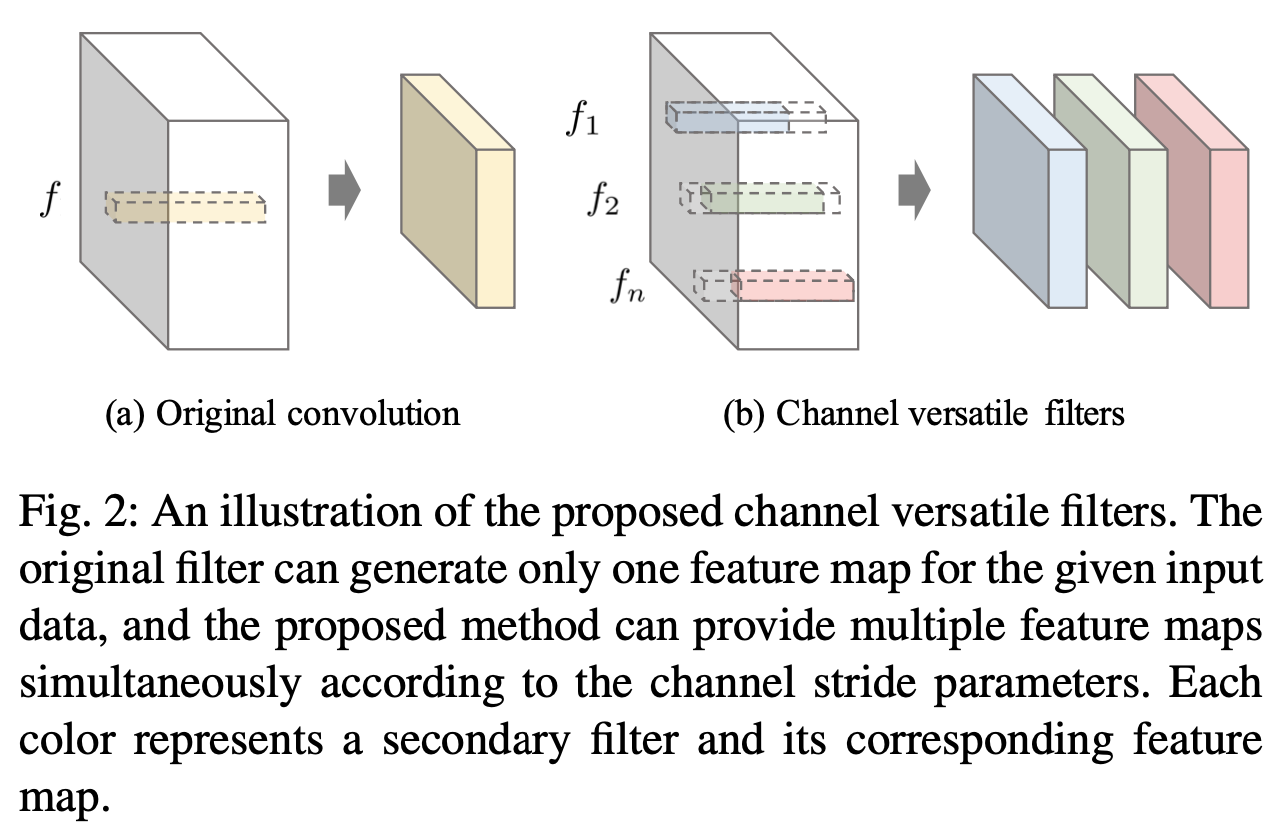
-
在卷积神经网络中 C >> H、W,所以在 Channel 方向设计多功能卷积非常必要
-
数学表示:
- y=[f^1 @ x1, ... ,f^n @ xn]
s.t. ∀i,f^i∈Rd×d×c, n=(c−c^)/g+1
- 其中:
- 省略 bias
- g means channel-wise stride
- c^ means non-zeros channels
- n means 一个 filter 用几次
- [] means concat
学习策略
mask 具体如何设计
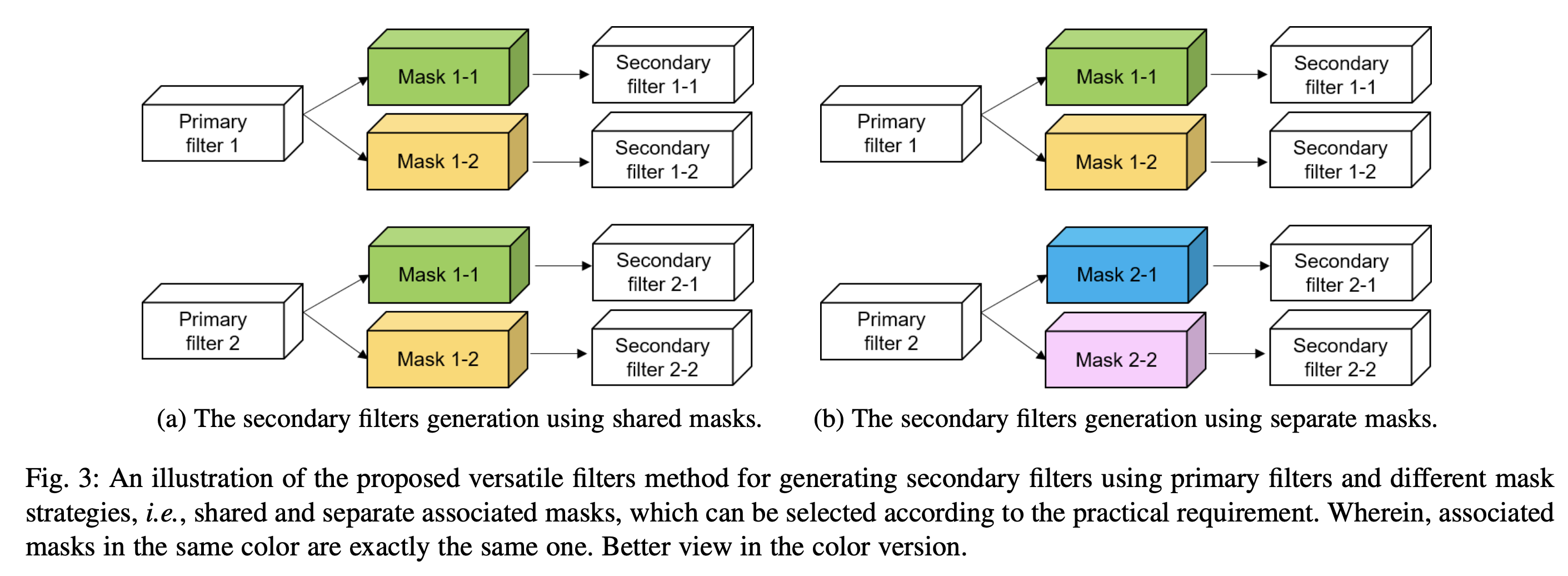
- mask 两种设计策略:
- 方案 a:每个主卷积核共享一套二值 mask
- 方案 b:每个二值 mask 只用一次
- 实验证明,方案 b 效果更好,原因是:方案 b 中二值 mask 的假设空间更大
如何让主卷积核对应的多个二值 mask 相似性
-
极端情况:如果一个主卷积核对应的所有二值 mask 都相同,那理论上模型效果与只是用主卷积核运算表现基本相同
-
所以需要加入一种使得 同一个主卷积核对应的多个每个二值 mask 更倾向不同 的损失函数
-
损失函数数学表示:
- minF,ML=L0(F,M)+λLortho(M)
- M=[vec(M1), ... ,vec(Ms)]
Lortho=21∥d2c1MTM−I∥F2
- 其中:
- Lortho means loss of Orthogonal(正交损失)
- L0 means 任务相关 loss
- Mi 表示一个主卷积核的一个二值 mask
- 正交矩阵的性质:
- 假设 M 是一个正交矩阵,则 MTM=I
- 正交矩阵的列向量线性无关
对主卷积核的优化方法
- 总 loss 包括 任务相关 loss 和 mask 正交 loss
- 只有 任务相关 loss 与主卷积核相关
- ∂fi∂L=∂fi∂L0=∑j=1s∂f^ij∂L0∘Mj
- ∂F∂L=[∂f1∂L0, .... ,∂fk∂L0]
- F←F−ηFL
对二值 mask 的优化方法
- 先将 Lortho 展开:
- Lortho=21Tr[(d2c1MTM−I)(d2c1MTM−I)T]=21Tr[d4c21MTMMTM−2d2c1MTM+I]
- 所以:
- ∂M∂Lortho=21(d4c24MMTM−d2c4M)=d4c22MMTM−d2c2M
- ∵ 交换门,∴∂Mj∂L0=∑i=1k∂f^ij∂L0∘fi
- ∂M∂L=[∂M1∂L0, ... ,∂Ms∂L0]+λ∂M∂Lortho
- 因为 M 是 binary 的离散值,所以需要一个代理的连续变量 H,实现 直通估计器 STE 的作用
- M=sign(H), H=clip(H,0,1)
- ∂M∂L=∂H∂L
- {H←MH←clip(H−η∂H∂L,0,1)

Thought
- 这篇文章在 2018 年就已经发表在 nips 上了,最近做了一些详细实验后重新挂在了 arxiv 上了
- 本文实验非常详细,虽然没有开源,前向计算和反向计算的数学推导很精彩~~(敲 latex 敲的想哭)~~,像一篇 survey
- 这篇文章 inference 阶段有点重参数化的感觉,RepMLP 思想和本文有点相似
- STE 部分让我想起了 DoReFa-Net 😂



