0%
URL
TL;DR
- 多任务模型共享网络结构,在一些弱关联或者负相关的任务上,可能出现 跷跷板效应(Seesaw Phenomenon),即一个任务的效果和另外一个任务的效果无法同时提升
- 针对跷跷板效应问题,本文提出一种
CGC(Customized Gate Control) 结构,任务之间部分共享底层网络
- 提出一种
CGC 的升级版本 - PLE(Progressive Layered Extraction)
- 单层网络结构
CGC 与多层网络结构 PLE 都优于 MMOE
Algorithm
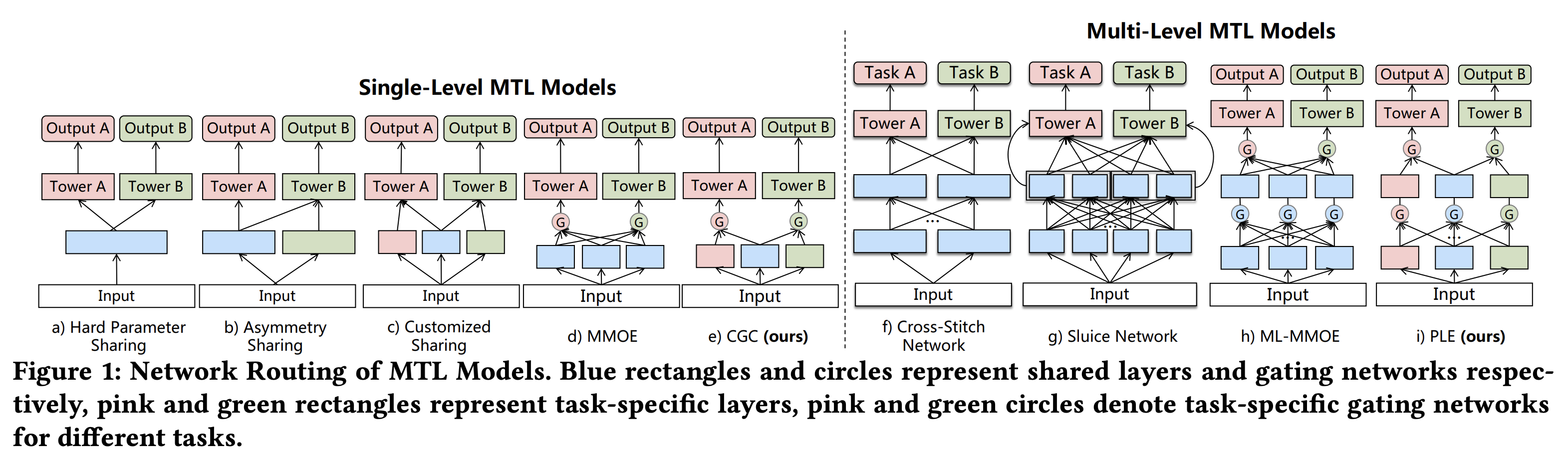
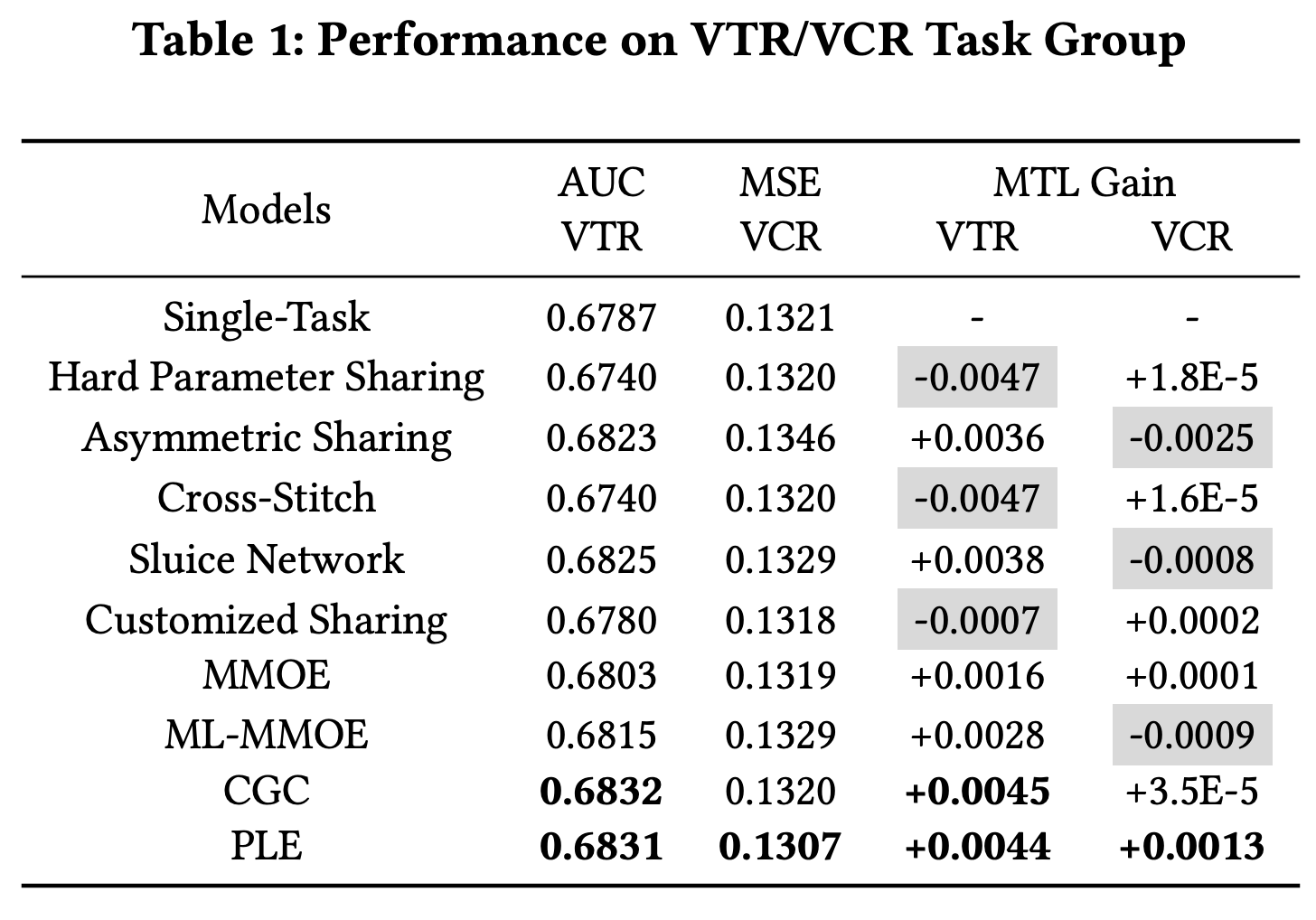
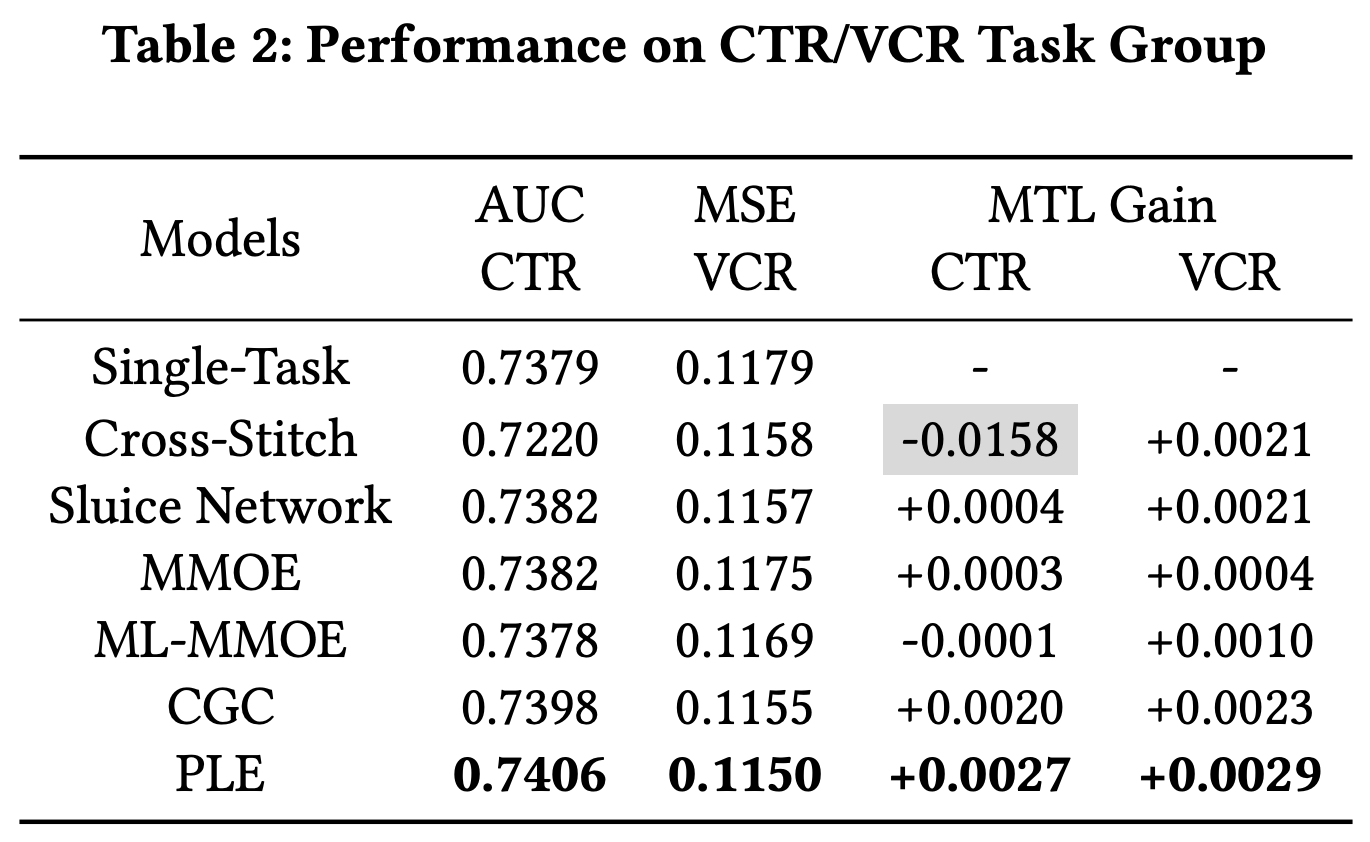
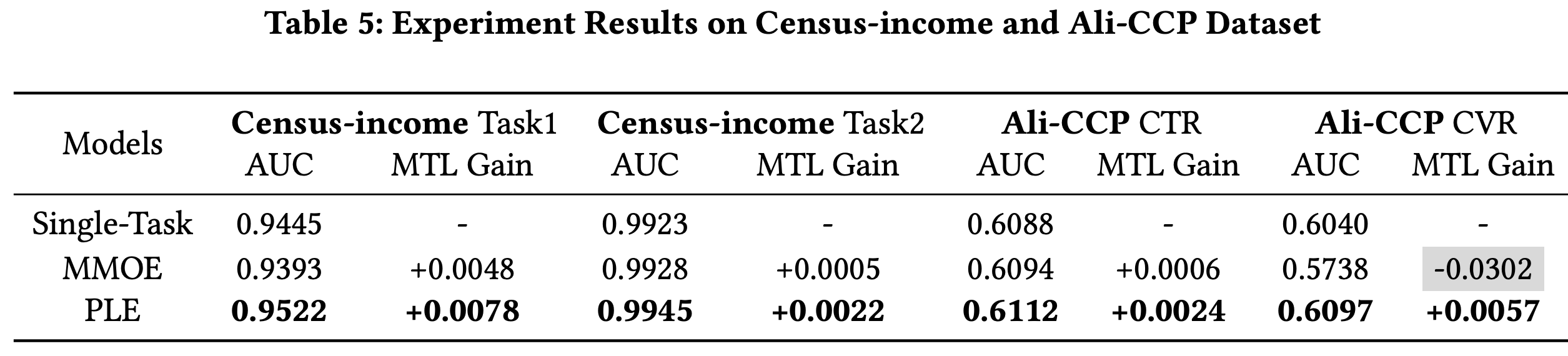
不同多任务网络结构对比
Customized Gate Control(CGC)
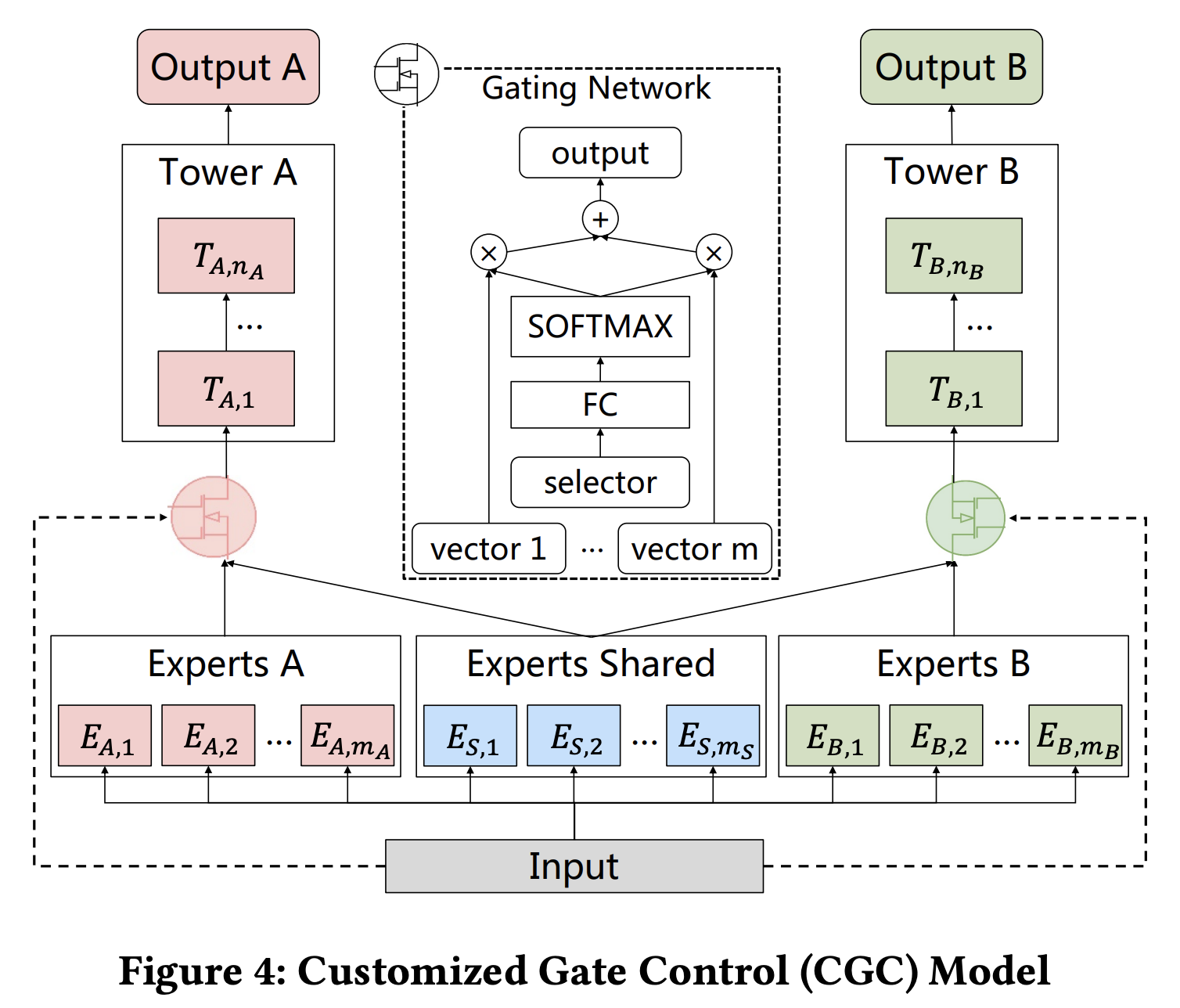
CGC 结构部分共享表征,部分独用表征,共享表征和独占表征的权重分配是通过门控制
yk(x)=tk(gk(x)),其中 tk 表示第 k 个任务的 tower
gk(x)=wk(x)Sk(x),其中 wk(x) 表示表征选择器 wk(x)∈Rmk+ms、mk、ms 分别表示独占和共享表征的数量
wk(x)=Softmax(wgkx),wgk∈R(mk+ms)×d,d 表示表征向量的长度
Sk(x)=[E(k,1)T,E(k,2)T,...,E(k,mk)T,E(s,1)T,E(s,2)T,...,E(s,ms)T],E 表示表征,Sk(x)∈Rd×(mk+ms) 表示表征集合
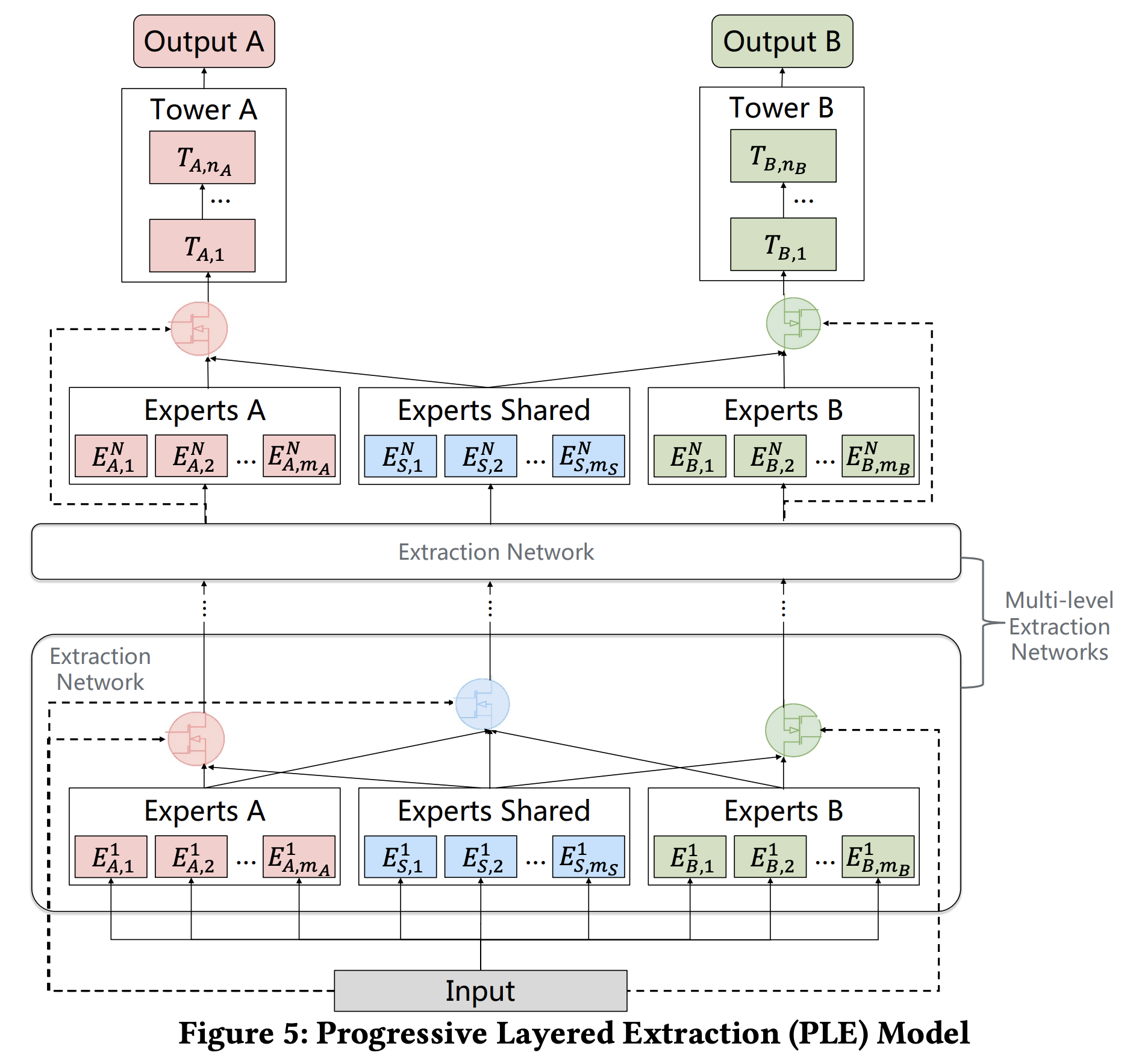
- PLE 相当于 CGC 的多层网络结构
yk(x)=tk(gk,N(x)),N 表示网络总层数
gk,j(x)=wk,j(gk,j−1(x))Sk,j(x)
效果对比
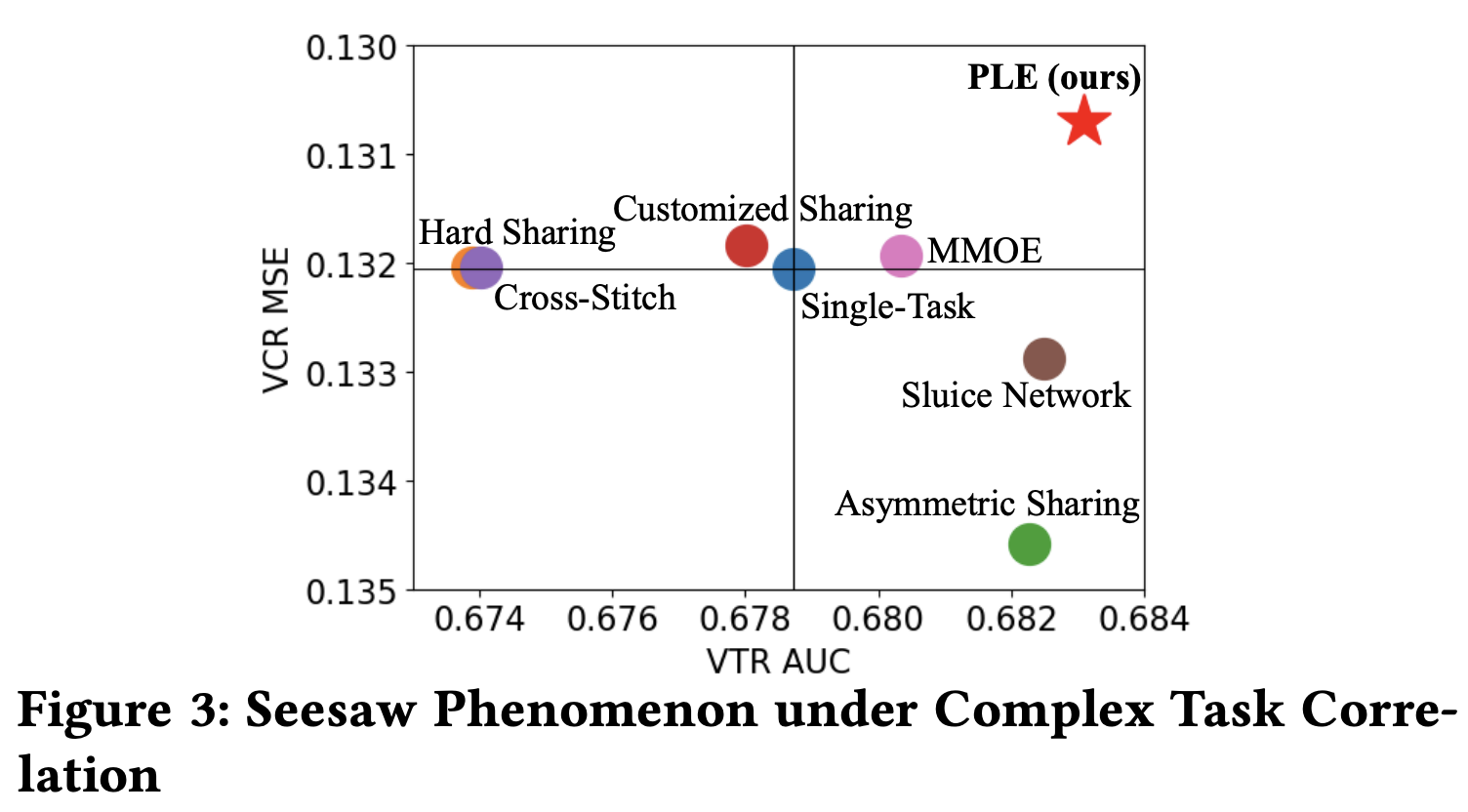
Thought
MMOE 的改进版,从效果来看,对于不正相关甚至互逆的任务,都可以有效解决跷跷板问题- 但本质还是更 general 的
MMOE,没有跳出 MMOE 对多任务的定义






