LSQ: Learned Step Size Quantization

URL

• https://arxiv.org/pdf/1902.08153.pdf

TL;DR

• 本文提出一种量化算法 LSQ，旨在通过学习的方式确定每一层量化的 scale
• LSQ 量化算法比基于统计确定 scale 的量化算法的（例如：DoReFa-Net）效果好

Algorithm

量化和反量化过程

• 量化过程：$\bar{v} = \lfloor clip(v/s, -Q_N, Q_p) \rceil$
• 反量化过程：$\hat{v} = \bar{v} \times s$

其中：

• $v$ 表示原始数据（weight / feature）
• $s$ 表示量化 scale
• $\lfloor \rceil$ 表示四舍五入（round）
• $-Q_N,\ Q_P$ 分别表示量化上下界，通常来说：
  • 对于无符号整形量化数据：$Q_N\ =\ 0,\ Q_P = 2^{b} - 1$
  • 对于有符号整形量化数据：$Q_N\ =\ 2^{b-1},\ Q_P = 2^{b-1} - 1$
• $\bar{v}$ 表示量化后的数据
• $\hat{v}$ 表示反量化（$\times s$）后的数据

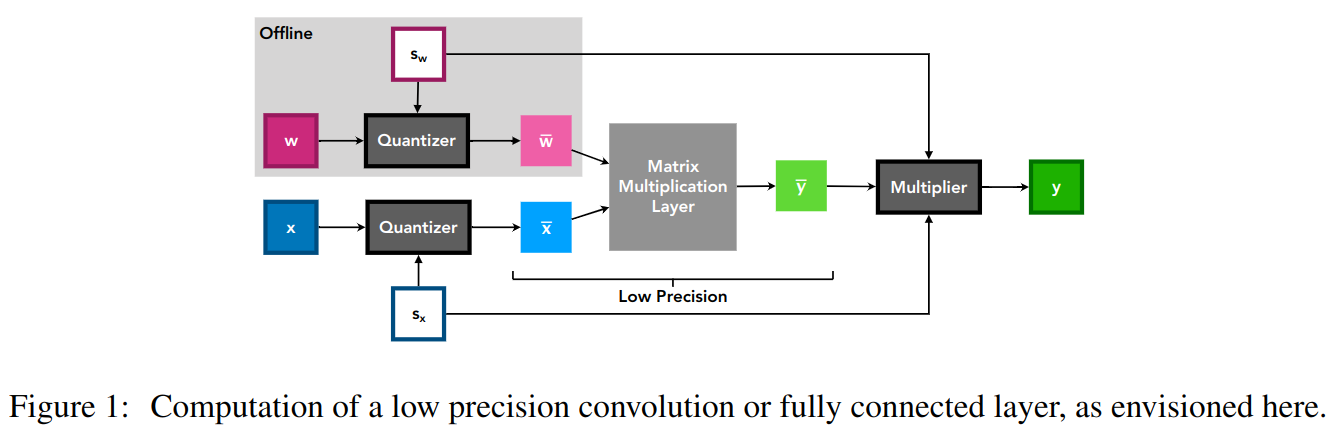
通常反量化会移到后面做，如上图中的 $s_x,\ s_w$ 在 $\bar{w}\ @\ \bar{x}$ 之后才会乘上去

对 scale 的梯度定义

$\frac{\partial\hat{v}}{\partial s} = \begin{cases} -v/s+ \lfloor v/s \rceil, & if\ -Q_N < V/s < Q_P\\ -Q_N, & if\ v/s \le -Q_N \\ Q_P, & if\ v/s \ge Q_P\end{cases}$

对量化区间外的部分有非常高的梯度，因为 clip 之后原始信息全部丢失。所以需要较大惩罚（梯度）。

• $\frac{\partial\hat v}{\partial v}=\begin{cases} 1, & if\ -Q_N<v/s<Q_P \\ 0, & otherwise\end{cases}$

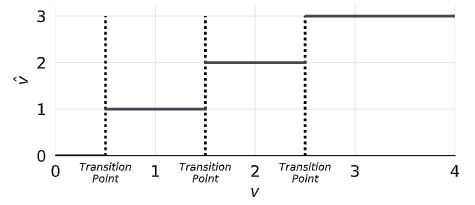
量化前数据和反量化后的数据关系

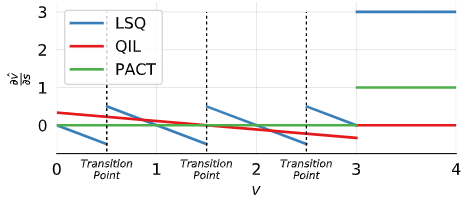
量化前数据和 scale 梯度的关系（有效将数据集中在量化点附近，减小量化损失）

• scale 的初始值 $\frac{2<|v|>}{\sqrt{Q_P}}$，其中 $<|v|>$ 表示输入的绝对值均值。

对 scale 的梯度上加的权重

• 训练中会涉及到 scale 的梯度、weight 的梯度和 feature 的梯度，需要均衡三个梯度，所以需要在weight 的梯度和 feature 的梯度上乘上两个因子进行平衡。
• $R = \frac{\nabla_sL}{s} / \frac{||\nabla_wL||}{||w||}$，需要 R 尽可能接近 1
• 经过数学推理和实验，得到两个权重因子 $g_w,\ g_f$ 分别表示 weight 梯度权重和 feature 的权重梯度。
• $g_w = \frac{1}{\sqrt{N_WQ_P}}\\ g_f = \frac{1}{\sqrt{N_FQ_P}}$，其中 $N_W,N_F$ 分别表示 number of weight 和 number of feature

一些实验 trick

• 越低位宽需要越低的 weight_decay 系数
• cosine learning rate decay 可以涨点
• 使用 float 模型去蒸馏可以涨点

Through

• 学出来的 scale 确实比统计出来的 scale 更 make sense ，毕竟 QAT 给了学习的机会，就多给些可学习的参数是有道理的。