Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

URL

paper: https://arxiv.org/pdf/2103.14030.pdf
code: https://github.com/microsoft/Swin-Transformer

TL;DR

本文提出一种新型 Transformer 结构使用 Window Multi-head Self-attention (W-MSA) 和 Shifted Window Multi-head Self-attention (SW-MSA) 结构替代原始 Transformer 使用的 Multi-head Self-attention (MSA) 结构。
- 大大节省了原始 Transformer 的计算复杂度。
- 在视觉任务中吊打了一众 CNN 和 Transformer。

Algorithm

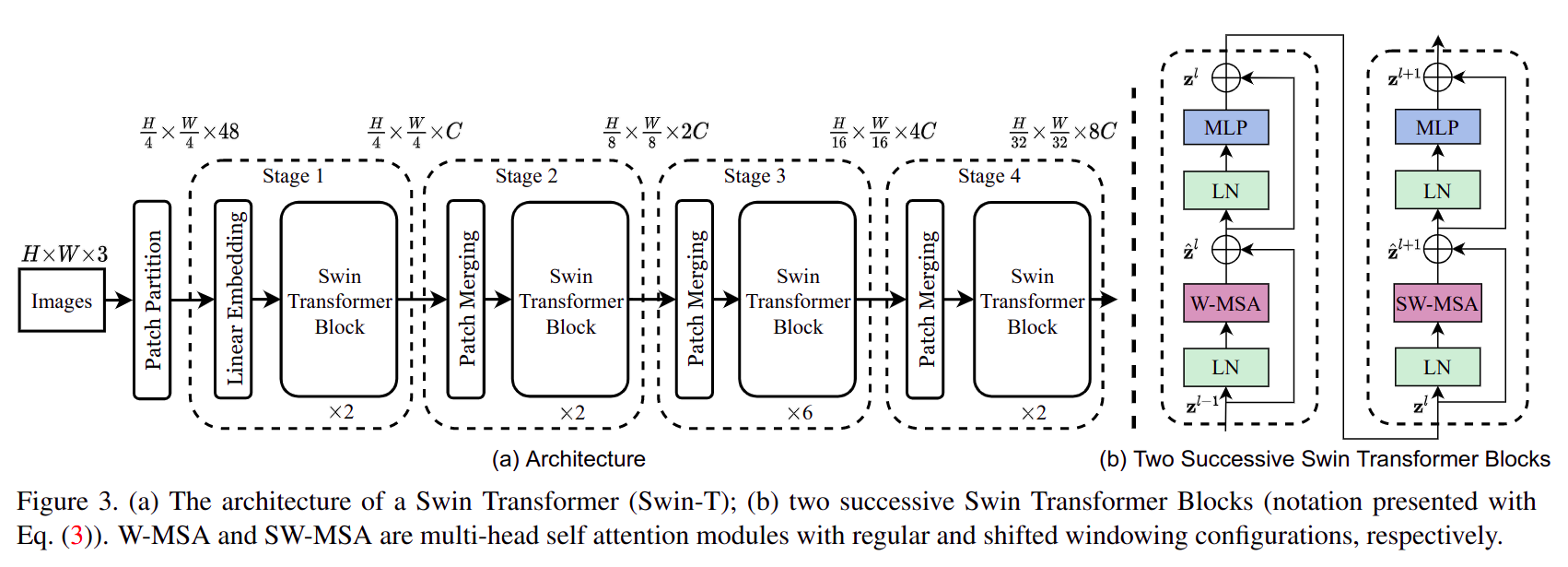
总体结构

swin-Transformer 总体按照类似 CNN 的层次化构建方式构建网络结构，分为 4 个 stage，每个 stage 都会将分辨率缩小一倍，channel 数扩大一倍 （like vgg） 。
Swin Tranformer Block 像大多数 Transformer Block 一样，不改变输入特征 shape，可以看做是一种比较高级（加入了 self-attention）的激活函数。
图中 Swin Tranformer Block 都是以连续偶数次出现，因为是一个 W-MSA Transformer Block + 一个 SW-MSA Transformer Block，如右边子图 b 所示。

Patch Partition

作用与 ViT 第一步很像：将图片切成若干等大小不重叠的 patch，patch_size = P，然后把每个 patch 从 (P, P, c) 拉成 1 维。
本实验中 patch_size = 4，所以一张图被裁切成了 $\frac{H}{4}\times\frac{W}{4}$ 个长度为 4 * 4 * 3 = 48 的向量。

Linear Embedding

与一个 shape = (48, C) 的矩阵乘将 48 维映射到 C 维。

与上一步结合可以变成一个 in_channel = 3, out_channel = C, kernel_size = stride = 4 的 Conv2d，官方实现中实际上也是这么做的（ class PatchEmbed ）。

Patch Merging

由两步组成，作用是 将分辨率缩小一倍，channel 扩大一倍。
- 将 $\frac{H}{4}\times\frac{W}{4}\times C$ 的输入使用 bayer2rggb (space2depth with block_size = 2) 变成 $\frac{H}{8}\times\frac{W}{8}\times 4C$ 。
- 再将 $\frac{H}{8}\times\frac{W}{8}\times 4C$ 与一个 $4C\times 2C$ 的矩阵相乘，输出一个 $\frac{H}{8}\times\frac{W}{8}\times 2C$ 的矩阵。

W-MSA

全称为 Windows Multi-head Self-attention，目的是为了减少 Self-attention 计算量。
- 原始的 MSA 会直接对完整输入计算其 self-attention 结果
- W-MSA 先将输入拆成大小为 $M\times M$ 且互不重叠的 windows，然后计算每个 window 的 self-attention 结果。
- 计算公式还是: $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
MSA 和 W-MSA 计算量对比（假设输入特征图 $X \in \mathbb{R}^{H\times W\times C}$ ，且 $W_q,W_k,W_v \in \mathbb{R}^{C\times C}$ ，且 Multi-head 的 head 数为 1)：
- MSA 计算量：
  - X -> Q / K / V 计算量： $\mathbb{R}^{H\times W\times C}\times \mathbb{R}^{C\times C}$ 计算量为 $3HWC^2$ 。
  - $QK^T$ 计算量： $\mathbb{R}^{HW\times C}\times \mathbb{R}^{C\times HW}$ 计算量为 $H^2W^2C$ 。
  - 不考虑 softmax 和 $\frac{..}{\sqrt{d_k}}$ 计算量。
  - softmax 结果 $\times V$ 计算量： $\mathbb{R}^{HW \times HW}\times \mathbb{R}^{HW \times C}$ 计算量为 $H^2W^2C$ 。
  - 因为需要 Multi-head，所以需要将 $\times V$ 之后的矩阵再 $\times W_o$ ，且 head 数为 1，计算量： $\mathbb{R}^{1*HW \times C}\times \mathbb{R}^{C \times C}$ 计算量为 $HWC^2$ 。
  - 总计算量： $4HWC^2 + 2H^2W^2C$ 。
- W-MSA 计算量：
  - 上图的 $H\rightarrow M,\ W\rightarrow M$ ，一共重复 $\frac{HW}{M^2}$ 次，所以总计算量为：
  $(4M^2C^2 + 2M^4C)\times \frac{HW}{M^2}=4HWC^2+2HWM^2C$
- 相比之下 W-MSA 会比 WSA 计算量少： $2HWC(HW-M^2)$ 。

SW-MSA

为了节省计算量 W-MSA 会将输入的完整特征图分 window，每个 window 独立去做 self-attention，这会导致 window 之间的关联性消失，这有悖于 self-attention 会在全图上建立长距离全局相关性依赖的特点。
所以，作者引入 SW-MSA 的方案通过滑窗解决这一问题。

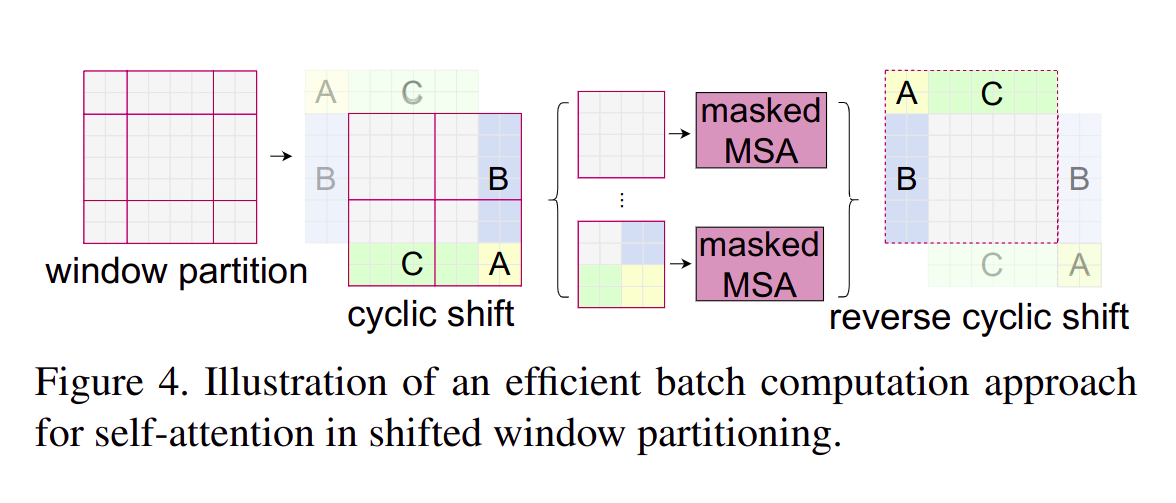
滑窗会带来边角处的零碎区域（长或宽小于 window_size 的区域），由于 $H \% M = 0,\ W \% M = 0$ (W-MSA 要求)，所以零碎的区域可以通过调整位置拼成完整 window 。
完整的滑窗区域与 W-MSA 一样独立做 Self-attention。
由零碎区域拼成的滑窗区域中：
- 本属于同一零碎区域的位置可以 Self-attention 。
- 本不属于同一零碎区域的位置在原图上不相邻，不能做 Self-attention 。
- 具体做法是来自不同区域位置之间的 Self-attention 被 mask 掉 ，只保留来自相同区域的位置间的 Self-attention 。

W-MSA + SW-MSA

如网络结构图子图 b 所示，W-MSA 连接 SW-MSA 之后，数学表示：

$\hat{z}^l=W-MSA(LN(z^{l-1})) + z^{l-1}$

$z^l=MLP(LN(\hat z^l)) + \hat z^l$

$\hat z^{l+1} = SW-MSA(LN(z^l))+z^l$

$z^{l+1} = MLP(LN(\hat z^{l+1}))+\hat z^{l+1}$

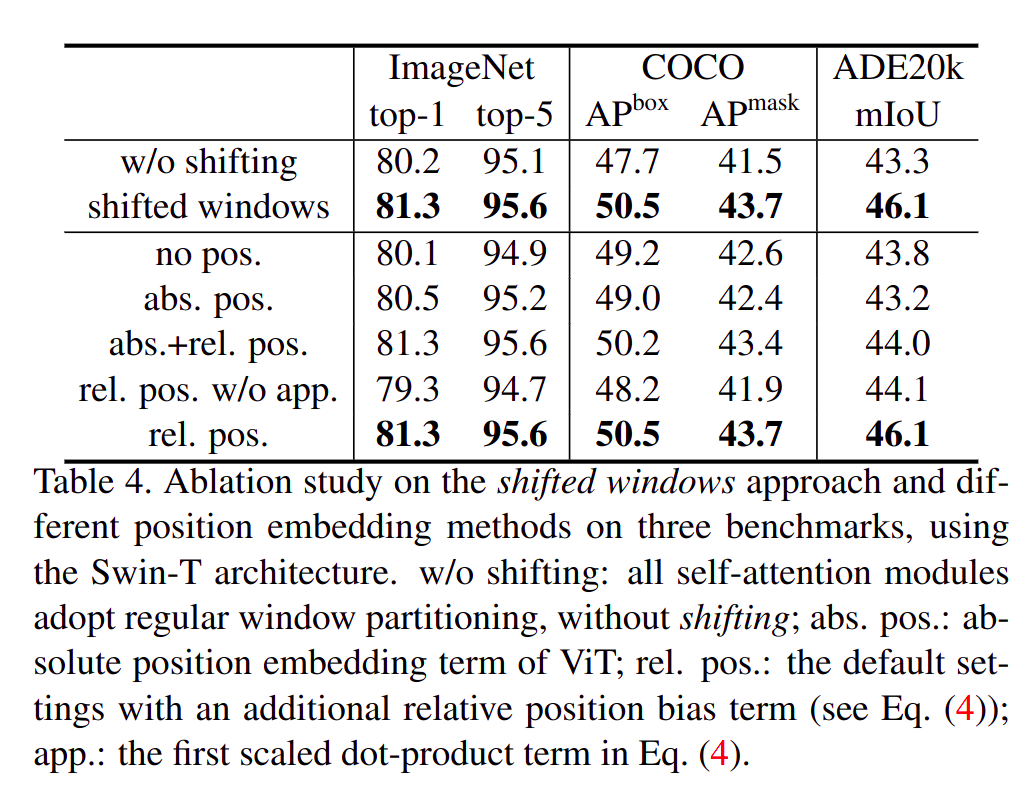
Relative Position Bias

对 Self-attention 加上 相对位置偏置 bias 之后，精度提升巨大。
原始 Self-attention： $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$ 。
Relative Position Bias Self-attention： $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}} + Bias)V$ 。

Through

质疑了很多人都没有质疑的点，例如给 Self-attention 加上相对位置偏置。
本质是对 Tranformer 的一种很 work 的加速方法。
但 Shift window 逻辑比较复杂，没有经典模型该有的简约美，盲猜之后会被更 make sense 的结构替代。