相机内参与外参

三种成像相关坐标系

• 像素坐标系：一种 2D 坐标，以图片左上角为原点，横轴（宽度方向）向右为 x 轴正方向，纵轴（高度方向）向下为 y 轴正方向，单位是像素
• 相机坐标系：一种 3D 坐标，以相机光心为原点，垂直相机平面远离相机方向为 z 轴正方向，垂直于 z 轴且平行于相机平面，水平向右为 x 轴正方向，竖直向下为 y 轴正方向，单位是米
• 世界坐标系：一种 3D 坐标，一种人为定义的，且x, y, z 轴两两垂直的坐标系，单位是米

相机内参

• 相机内参可以实现像素坐标系与相机坐标系之间相互转换，通常使用一个 3 * 3 矩阵表示
  
  

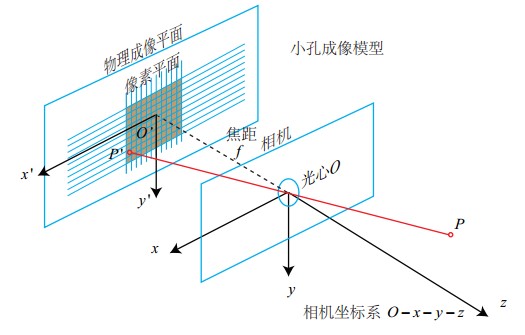
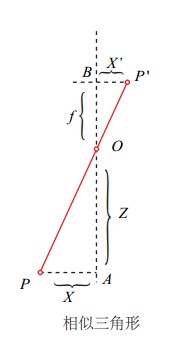
• 根据小孔成像和相似三角形原理，可以得出相机坐标系与成像坐标系点的对应关系：$\frac{Z}{f}=\frac{X}{x}=\frac{Y}{y}$
  其中：$(X,Y,Z)$ 为相机坐标系下的点的坐标， $(x, y)$ 为投影到成像平面上的点的坐标， $f$ 表示焦距。

• 再根据成像坐标系到像素坐标系的对应关系：

  $$\begin{matrix} u=\alpha \cdot x + c_x \\ v = \beta \cdot y + c_y \end{matrix}$$

  其中：

  • $\alpha,\beta$ 分别表示 $x, y$ 方向上成像宽度到像素宽度的投影
  • 由于成像坐标系原点为成像中心，像素坐标系原点为像素左上角，所以需要加上原点的偏移， $c_x,c_y$ 分别表示 $x, y$ 方向上原点的偏移。

• 所以，相机坐标系 $(X,Y,Z)$ 与像素坐标系 $(u, v)$ 可通过相机内参相互转换：

  $$Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}X\\ Y\\ Z \end{bmatrix}$$

  其中： $f_x=\alpha \cdot f,\ f_y=\beta \cdot f,\ Z$ 表示相机坐标系下的深度

• $\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$ 被称为相机内参 $K$

相机外参

• 相机外参可以实现相机坐标系与世界坐标系之间相互转换（刚体变换），通常用一个 3 * 3 的旋转矩阵 $R$ 和一个 3 * 1 的平移矩阵 $T$ 表示：

  $$\begin{bmatrix} X_c\\ Y_c \\ Z_c \end{bmatrix}=\begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} X_w\\ Y_w \\ Z_w \end{bmatrix} + \begin{bmatrix} T_{1} \\ T_{2} \\ T_{3} \end{bmatrix}$$

  其中： $(X_c,Y_c,Z_c)$ 表示相机坐标系下的点， $(X_w,Y_w,Z_w)$ 表示世界坐标系下的点

• 齐次化之后，得到一个 4 * 4 的矩阵：

  $$\begin{bmatrix} X_c\\ Y_c \\ Z_c \\ 1\end{bmatrix}=\begin{bmatrix} R_{11} & R_{12} & R_{13} & T_1 \\ R_{21} & R_{22} & R_{23} & T_2 \\ R_{31} & R_{32} & R_{33} & T_3 \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} X_w\\ Y_w \\ Z_w \\ 1\end{bmatrix}$$

总结

• $camera\ intrisic\ matrix \times camera\ coordinate\ system = depth\ in\ camera\ coordinate system \cdot image\ coordinate\ system$
• $camera\ extrisic\ matrix \times world\ coordinate\ system = camera\ coordinate\ system$
• $camera\ intrisic\ matrix \times camera\ extrisic\ matrix \times world\ coordinate\ system = depth\ in\ camera\ coordinate system \cdot image\ coordinate\ system$