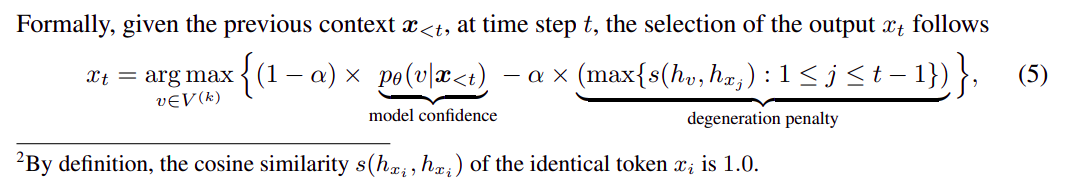A Contrastive Framework for Neural Text Generation

URL

TL;DR

本文提出一种叫做 Contrastive search 的解码方法，比 top-k / top-p 等随机解码方法和 argmax 这种贪心解码方法更优，模型输出内容语意更连贯，模型更不容易退化
Contrastive search 是在 top-k 基础上增加了 degeneration penalty（退化惩罚项），算是 random sampling 类算法的升级版
但需要将候选的 top-k 输出追加到序列末尾作为输入重新输入到模型中输出 top-k 对应的 hidden state，因此时间复杂度较高

Algorithm

总体架构

其中 $\alpha$ 是超参数，用来平衡模型预测结果和退化惩罚项
h 表示 hidden state，用 $h_v$ 和序列中每一个 token 的 hidden state 计算相似度
由于 $h_v$ 只能在下一次 inference 时产生，所以需要在 decoding 阶段再推理一次，这一步比较麻烦

用一段代码来描述一下解码过程

首先在 t-1 时刻输入 seq_len 长度的序列，输出 vocab_size 长度的 logits，选 top-k

# compute the logits in this step
prev_hidden_states, logits = model.compute_logits_and_hidden_states(input_ids)
_, seqlen, embed_dim = prev_hidden_states.size()
_, _, vocab_size = logits.size()

logit_for_next_step = logits[:,-1,:]
assert logit_for_next_step.size() == torch.Size([1, vocab_size])

# normalize with the softmax function
next_probs = F.softmax(logit_for_next_step, dim = -1)
assert next_probs.size() == logit_for_next_step.size()

# collecte top-k candidate tokens and their logits (model confidence)
_, next_top_k_ids = torch.topk(logit_for_next_step, dim = -1, k = beam_width)
assert next_top_k_ids.size() == torch.Size([1, beam_width])
        
next_top_k_probs = torch.gather(next_probs, dim = 1, index=next_top_k_ids)
assert next_top_k_probs.size() == next_top_k_ids.size()

将 top-k 预测的每一种可能追加到原始序列，并在 batch size 维度 concat 成一个 shape = [beam_width, seq_len + 1, dim] 的输入

# concatenate each candidate token with prefix
expanded_context = [input_ids for _ in range(beam_width)]
expanded_context = torch.cat(expanded_context, dim = 0)
assert expanded_context.size() == torch.Size([beam_width, seqlen])
top_k_ids = top_k_ids.view(beam_width, 1)
next_input_ids = torch.cat([expanded_context, top_k_ids], dim = -1)
assert next_input_ids.size() == torch.Size([beam_width, seqlen+1])

将 shape = [beam_width, seq_len + 1, dim] 输入到模型中，计算得到每个 token 的 hidden state

# feed these candidates into next round to get their hidden states
new_hidden_states, next_logits = model.compute_logits_and_hidden_states(next_input_ids)
assert new_hidden_states.size() == torch.Size([beam_width, seqlen+1, embed_dim])
context_hidden = new_hidden_states[:,:seqlen,:]
assert context_hidden.size() == torch.Size([beam_width, seqlen, embed_dim])
next_hidden = new_hidden_states[:,seqlen:,:]
assert next_hidden.size() == torch.Size([beam_width, 1, embed_dim])

计算每一个 next hidden state 和 context hidden state 之间的相关性，相关性越高，说明重复性越高，惩罚越重，选择此 token 作为 next input id 的可能性越低

def ranking(context_hidden, next_hidden, next_top_k_ids, next_top_k_probs, alpha):
    '''
        context_hidden: beam_width x context_len x embed_dim
        next_hidden: beam_width x 1 x embed_dim
        next_top_k_ids: beam_width x 1
    '''
    beam_width, context_len, embed_dim = context_hidden.size()
    assert next_hidden.size() == torch.Size([beam_width, 1, embed_dim])
    norm_context_hidden = context_hidden / context_hidden.norm(dim=2, keepdim=True)
    norm_next_hidden = next_hidden / next_hidden.norm(dim=2, keepdim=True)
    cosine_matrix = torch.matmul(norm_context_hidden, norm_next_hidden.transpose(1,2)).squeeze(-1)
    assert cosine_matrix.size() == torch.Size([beam_width, context_len])
    scores, _ = torch.max(cosine_matrix, dim = -1)
    assert scores.size() == torch.Size([beam_width])
    next_top_k_probs = next_top_k_probs.view(-1)
    scores = (1.0 - alpha) * next_top_k_probs - alpha * scores 
    _, selected_idx = torch.topk(scores, k = 1)
    assert selected_idx.size() == torch.Size([1])
    selected_idx = selected_idx.unsqueeze(0)
    assert selected_idx.size() == torch.Size([1,1])
    next_id = torch.gather(next_top_k_ids, dim = 0, index=selected_idx)
    assert next_id.size() == torch.Size([1,1])
    return next_id

Thought

道理上讲得通，但多推理的一次是实实在在的计算代价，总计算量直接翻倍，真的会有大模型选择这种解码方式吗？