On the Generalization of SFT: A Reinforcement Learning Perspective with Reward Rectification

URL

• paper: https://arxiv.org/pdf/2508.05629
• code: https://github.com/yongliang-wu/DFT

TL;DR

• 本文证明传统 SFT 过程常用的 Cross Entropy Loss 的梯度等价于 Reinforcement Learning 中策略梯度更新，但隐含一个病态的奖励结构：稀疏奖励和逆概率权重结合，导致 模型对低概率样本过拟合。
• 解决方案特别简单：在每个 token 的损失前乘当前 token 的概率作为权重。

Algorithm

公式角度

• 传统 SFT 过程的损失函数：

$$\nabla_{\boldsymbol{\theta}}\mathcal{L}_{\mathrm{SFT}}(\boldsymbol{\theta}) = - \mathbb{E}_{x,y \sim \pi_{\boldsymbol{\theta}}} \left[ \underbrace{\frac{1}{\pi_{\boldsymbol{\theta}}(y \mid x)}}_{\text{逆概率权重}} \cdot \underbrace{\mathbb{1}[y = y^{*}]}_{\text{稀疏奖励}} \cdot \nabla_{\boldsymbol{\theta}} \log \pi_{\boldsymbol{\theta}}(y \mid x) \right]$$

• DFT 损失函数：

$$\mathcal{L}_{\mathrm{DFT}} = - E_{\left(x, y^{*}\right)\sim\mathcal{D}} \sum_{t=1}^{\left|y^{*}\right|} \mathrm{sg}\left(\pi_{\theta}\left(y_{t}^{*}\mid y_{<t}^{*},x\right)\right) \log\pi_{\theta}\left(y_{t}^{*}\mid y_{<t}^{*},x\right)$$

• 注意：这里的 sg 是 stop gradient 操作，即不计算梯度 对应 pytorch 中常用的 .detach() 操作。

代码角度

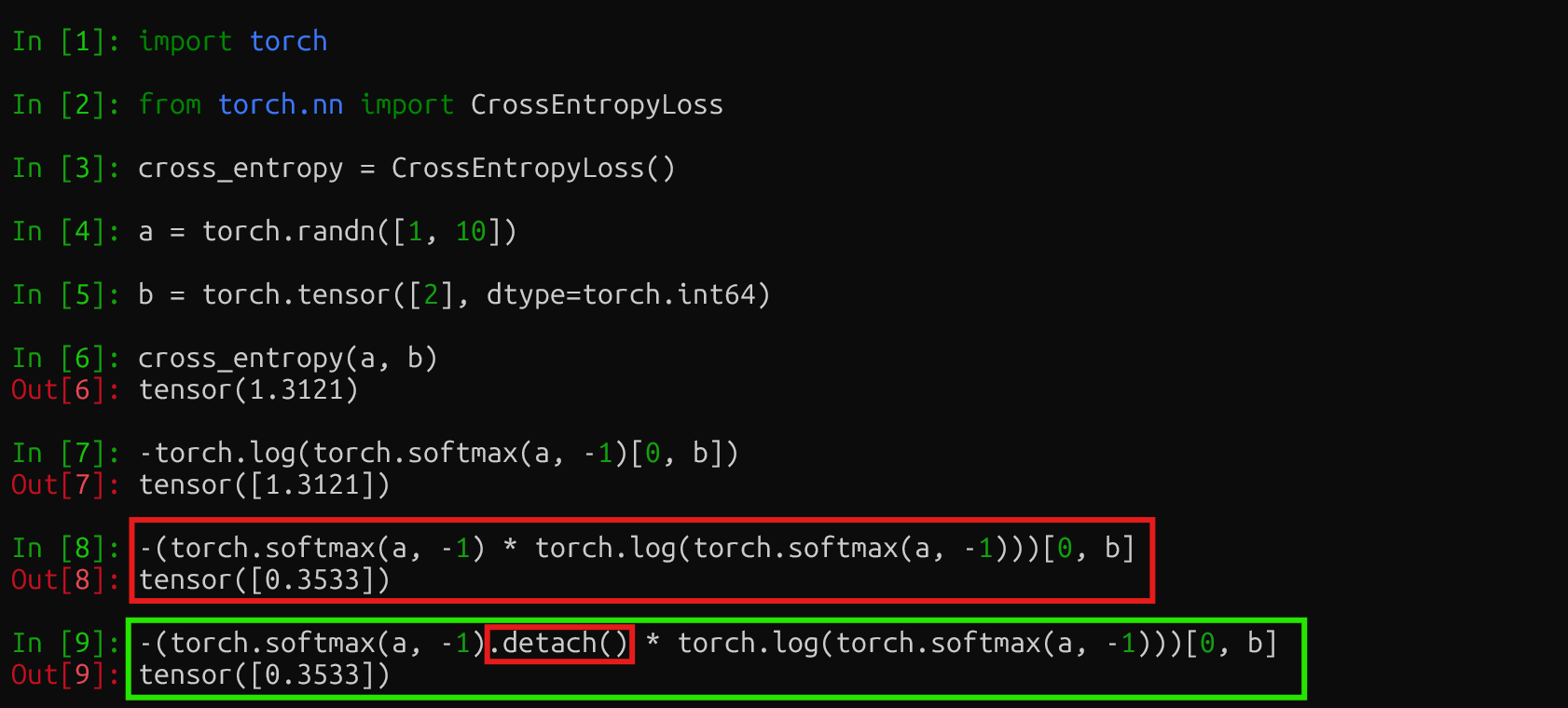
• a 表示预测序列中某个位置的的 logits
• b 表示对应位置的 GT
• cross entropy loss 就是 -log(softmax(a))[b]
• DFT 损失函数就是 -(softmax(a) * log(softmax(a)))[b]，但注意要 stop gradient，softmax(a) 只作为系数，反向传播不优化。

函数角度

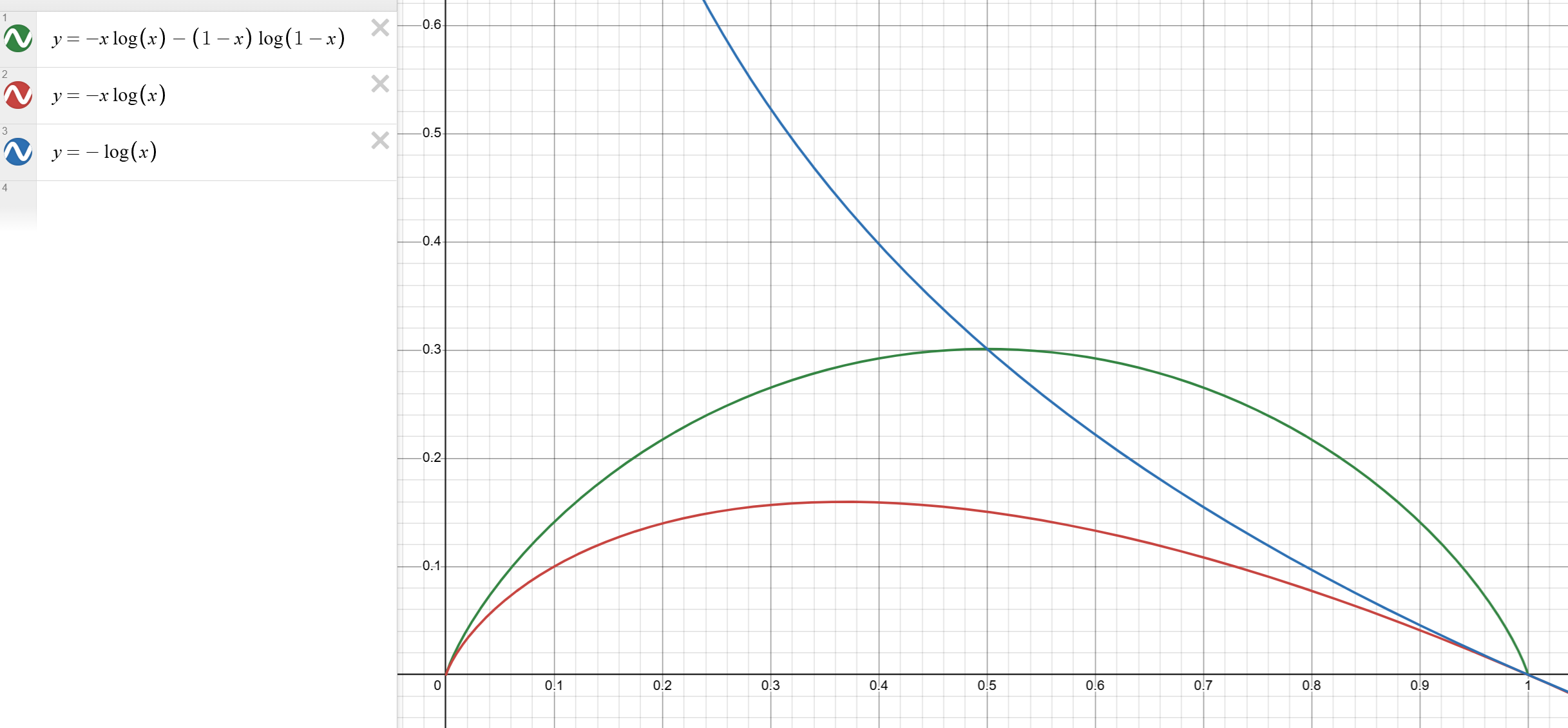
• 蓝色是标准 SFT 过程的损失函数（交叉熵）
• 红色是本文提出的 DFT 损失函数
• 绿色是我自己脑补的 DFT 函数扩展之后的损失函数，优点是比 DFT 对称性更好，效果怎么样不知道…
• 从函数角度看，SFT 在某个位置 GT 非常冷门的情况下，-log(softmax(a)) 会趋向于 inf，导致模型对这个冷门的 token 做了过大的参数更新，这是不合理的（因为模型已经经过了预训练，用非常低的概率预测 GT 说明这个 GT 可能是噪声）。
• 而 DFT 的函数可以看出，模型 优先关注不过分难或过分简单的 token，太难的可能是数据噪声，太简单的本身就没什么好学的。

Thoughts

• 从函数角度看：太难的我不学，因为太难；太简单的我不学，因为太简单。
• 郭德纲：我有四不吃…😂😂😂