URL
TL;DR
- 本文提出一种单步图像生成的算法
drifting,可以做到一步从噪声得到图片,无需像 diffusion / flow matching 一样多轮迭代得到图片
Algorithm
损失函数设计
L=Eϵ⎣⎢⎢⎢⎡∥∥∥∥∥∥∥∥predictionfθ(ϵ)−frozen targetstopgrad(fθ(ϵ)+Vp,qθ(fθ(ϵ)))∥∥∥∥∥∥∥∥2⎦⎥⎥⎥⎤
- ϵ 是随机噪声
- fθ() 是生成模型
- Vp,qθ 是漂移场
漂移场的计算
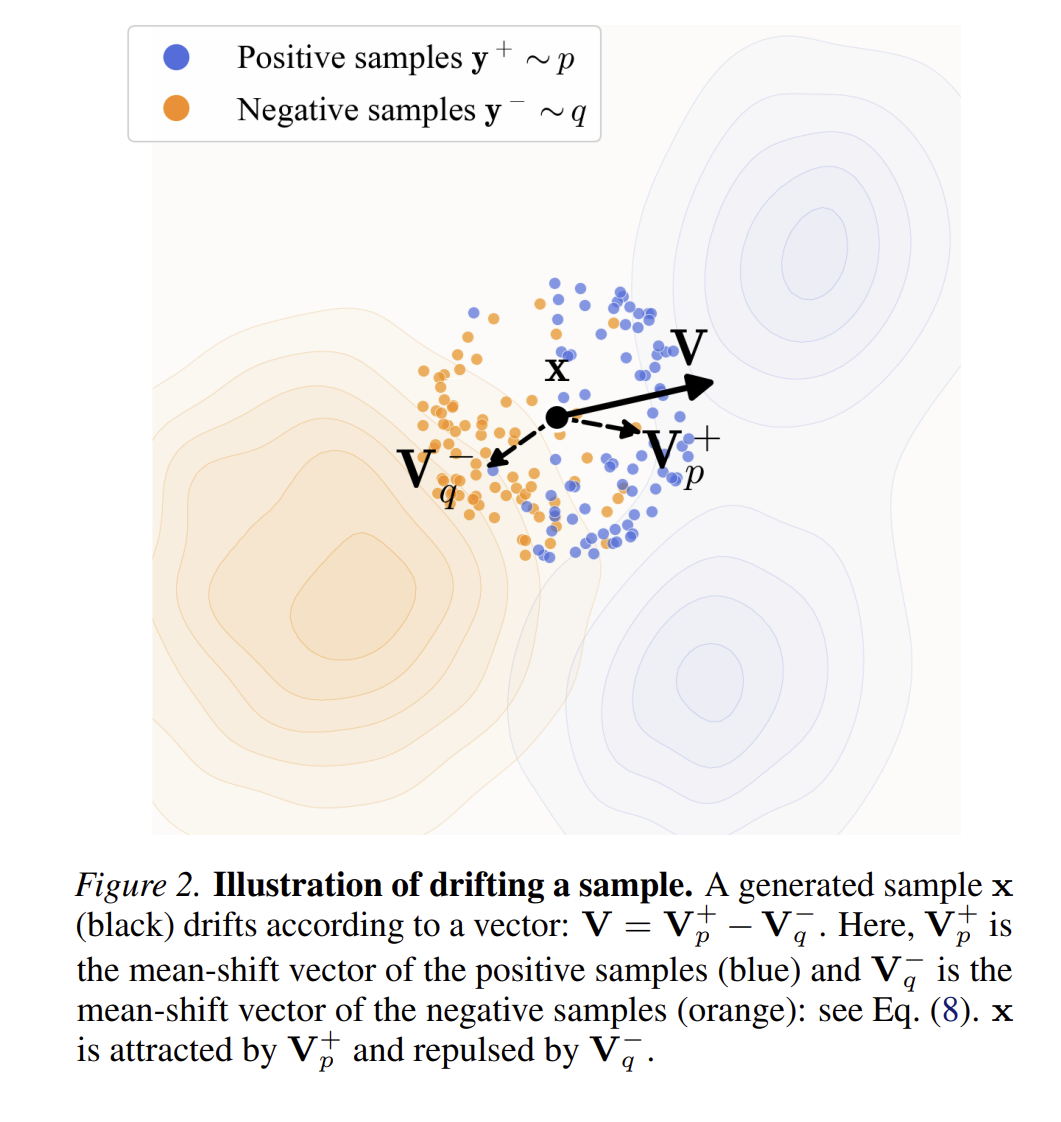
Vp,q(x)=正样本吸引Vp+(x)负样本排斥−Vq−(x)
- p 表示真实数据分布
- q 表示模型生成的数据分布
正样本吸引(来自真实数据)
Vp+(x)=Zp1Ey+∼p⎣⎢⎡标量权重k(x,y+)向量方向(y+−x)⎦⎥⎤
负样本排斥(来自生成分布)
Vq−(x)=Zq1Ey−∼q⎣⎢⎡标量权重k(x,y−)向量方向(y−−x)⎦⎥⎤
- y+ 真实样本
- y− 生成样本
- k(x,y) 相似度核函数,输出标量
相似度核函数
k(x,y)=exp(−τ∥x−y∥)

用一个例子说明损失函数的作用方式
x=(0,0)
y1+=(2,0), y2+=(2,2)
- 负样本(来自生成分布 q)两个点(通常就是 batch 里的其他生成样本)
y1−=(−1,0), y2−=(0,−1)
Step 1: 算 kernel 权重(谁更“像” x)
- 正样本的权重
- 距离:
- ∥x−y1+∥=2
- ∥x−y2+∥=8≈2.83
- kernel:
- k(x,y1+)=e−2≈0.135
- k(x,y2+)=e−2.83≈0.059
- 负样本的权重:
- k(x,y1−)=k(x,y2−)=e−1≈0.368
Step 2: 算方向向量(往哪里走)
y1+−x=(2,0)y2+−x=(2,2)
y1−−x=(−1,0)y2−−x=(0,−1)
Step 3: 算正向漂移 Vp+
∑k(x,y+)(y+−x)=0.135(2,0)+0.059(2,2)=(0.388,0.118)
Zp=0.135+0.059=0.194Vp+(x)=0.1941(0.388,0.118)≈(2.0,0.61)
Step 4: 算负向漂移 Vq−
Vq−(x)=(−0.5,−0.5)
Step 5: 合并成为最终漂移 Vp,q
Vp,q(x)=Vp+−Vq−=(2.0,0.61)−(−0.5,−0.5)=(2.5,1.11)
每个模块的组成
Generator: 采用 DiT (Diffusion Transformer) 架构。输入是噪声 + 类别条件。Tokenizer: 使用 Stable Diffusion 的 VAE 将图像压缩到 Latent Space (32×32×4)。Conditioning: 使用 AdaLN-Zero (Adaptive Layer Norm) 注入类别信息。这与标准 DiT 一致。Feature Extractor: 用于计算损失函数。论文指出损失是在特征空间中计算的,而非直接在像素空间。用的模型是 MAE 自监督训练得到的。
Thoughts
- 有很多
MoCo 的影子,比如 stop_grade 作为监督,对比学习等
- 还有
MAE,kaiming 大佬把自己的作品都串起来了,tql…

