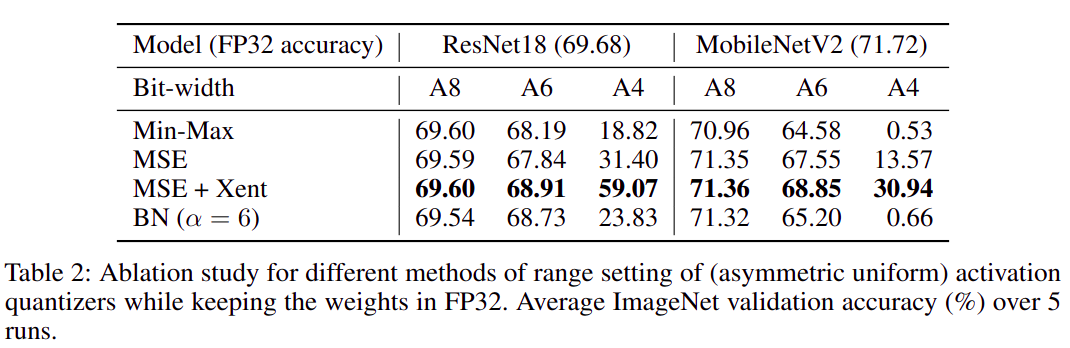
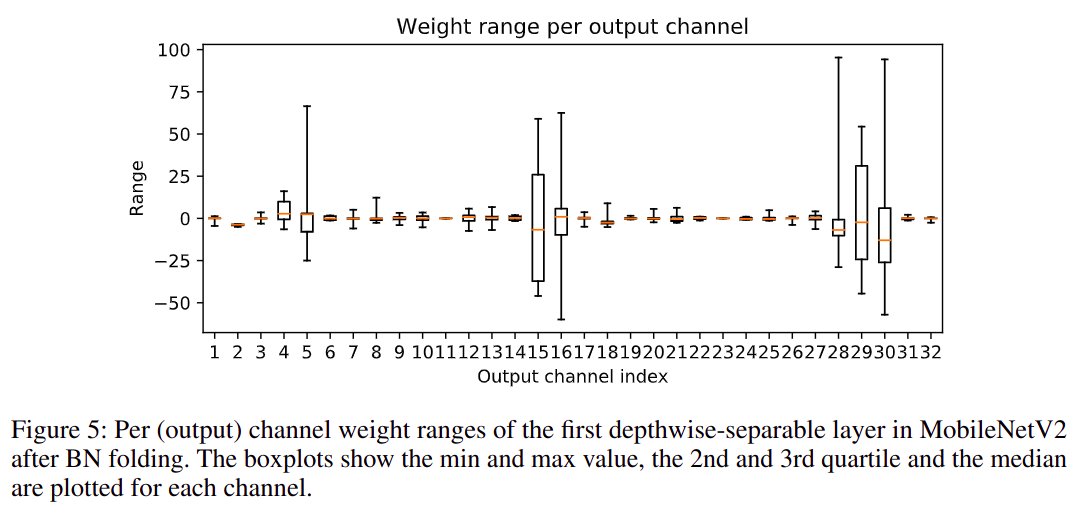
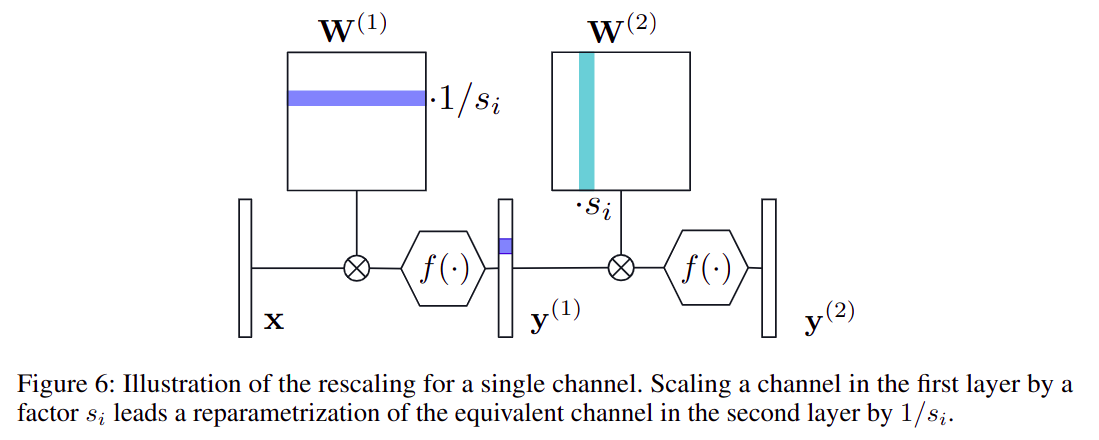
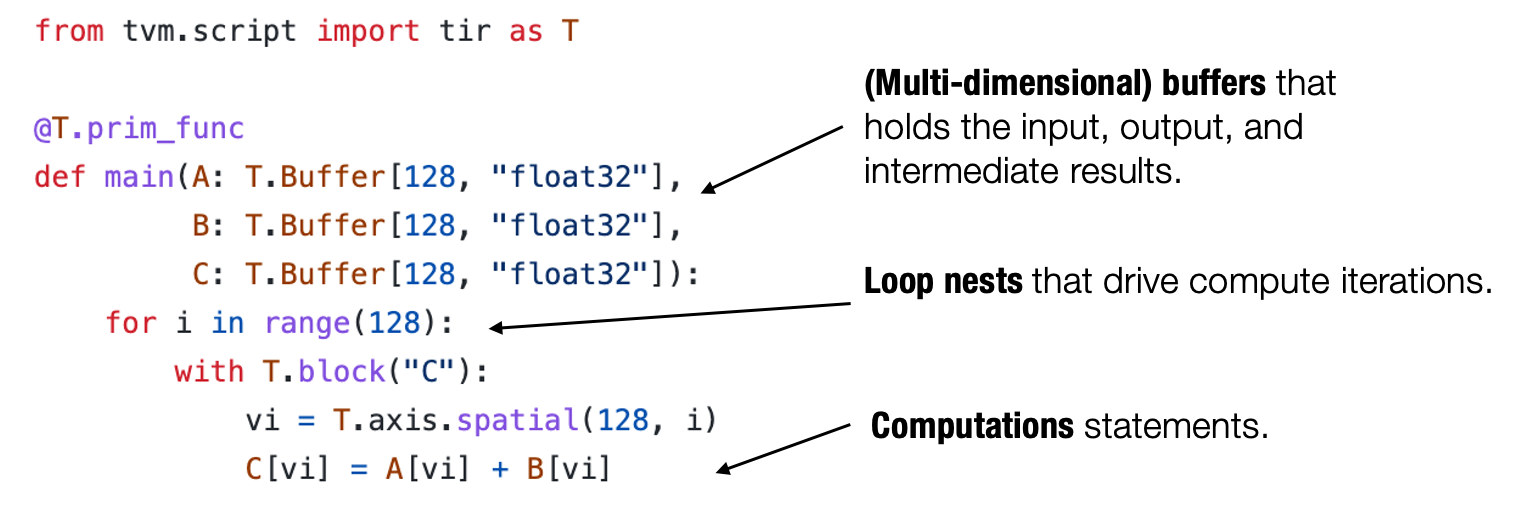
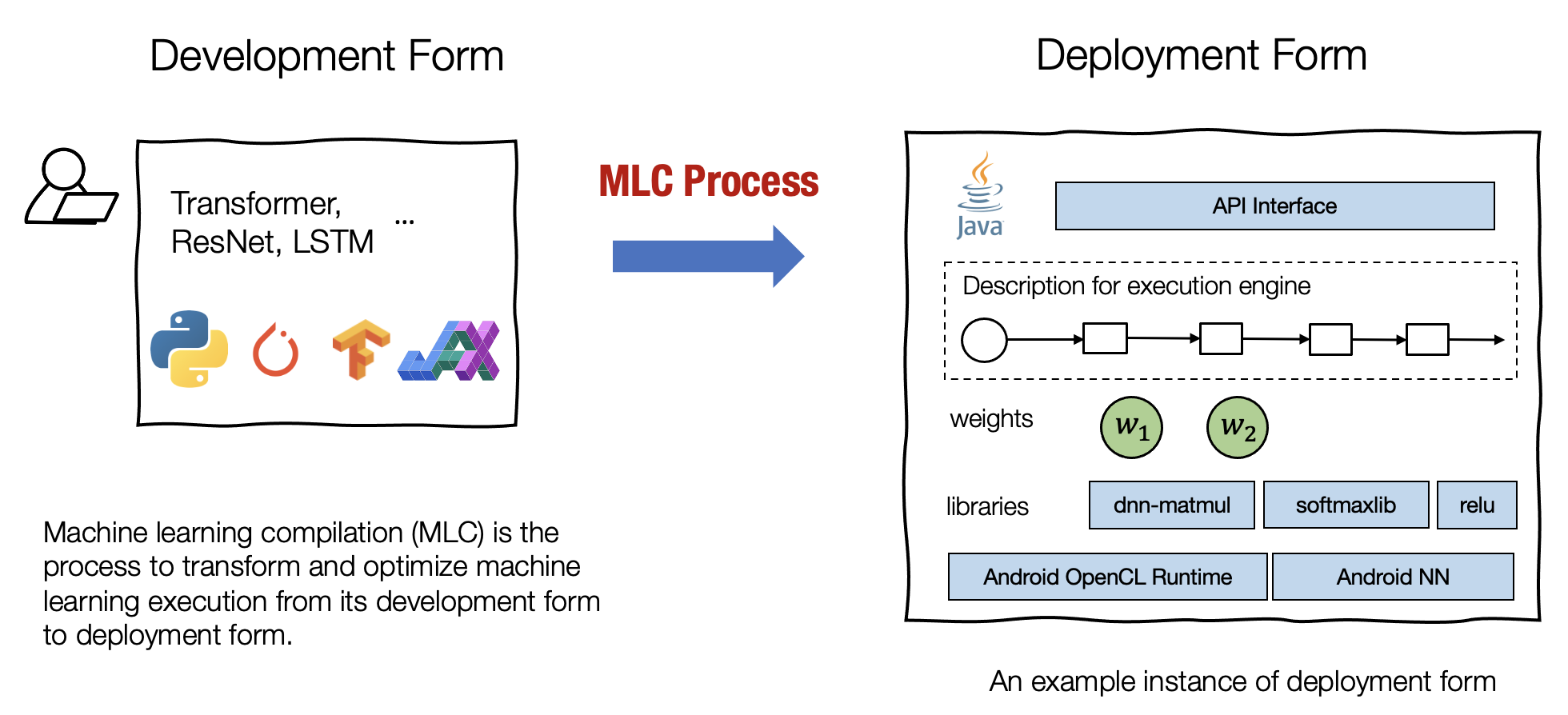
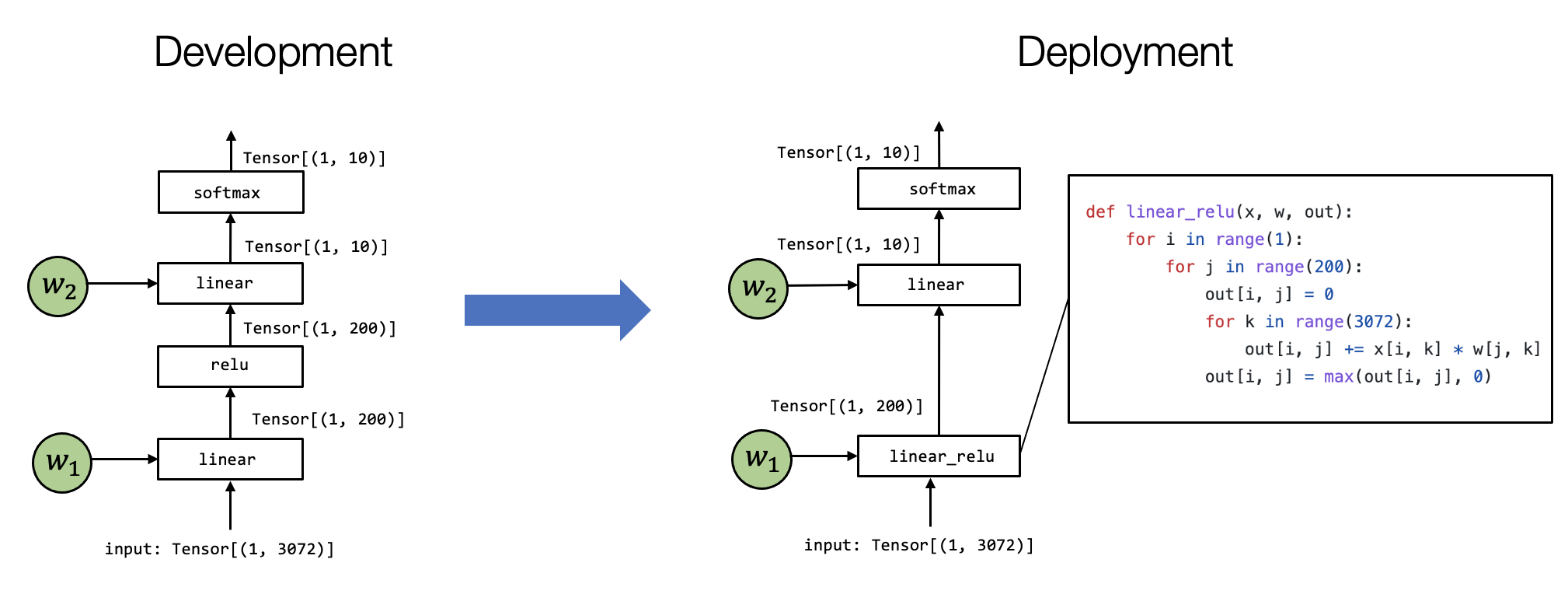
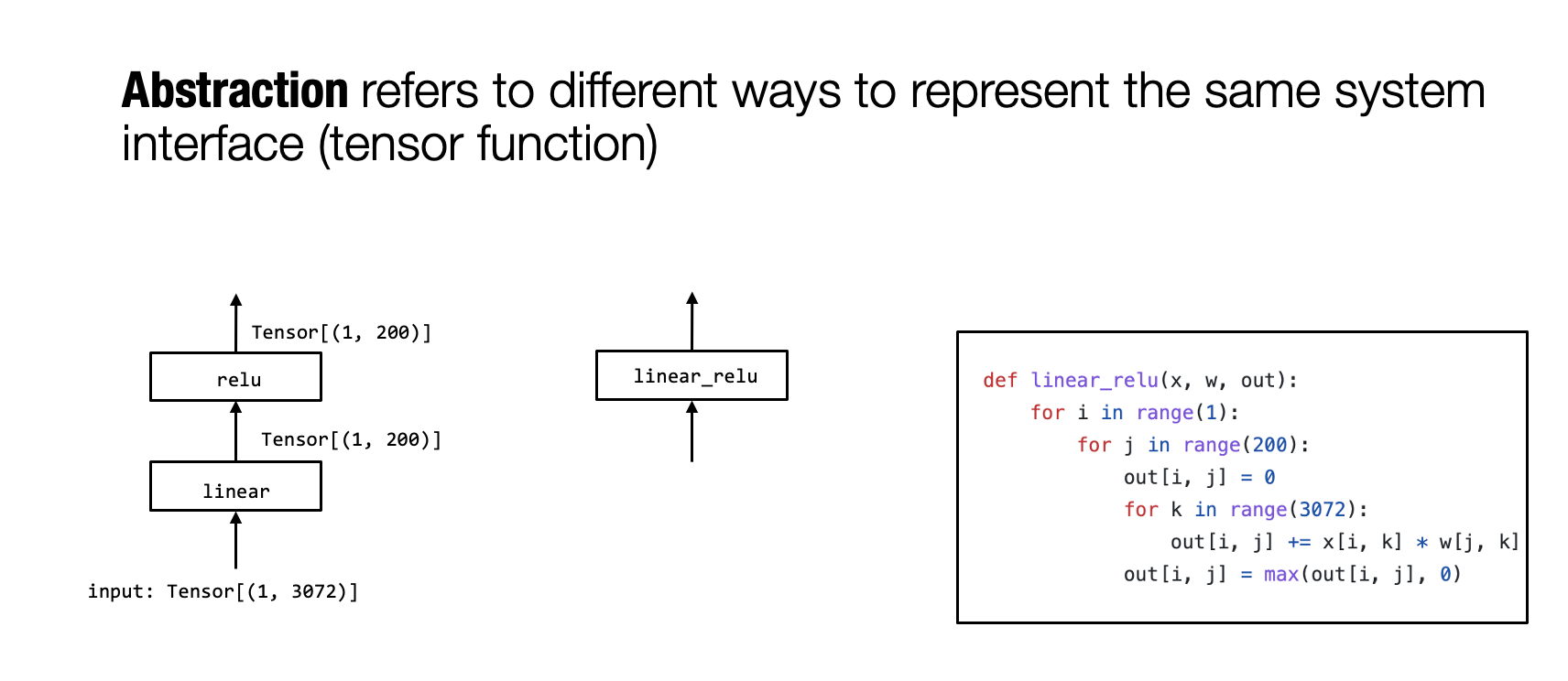
Python 闭包 (closure)
闭包定义
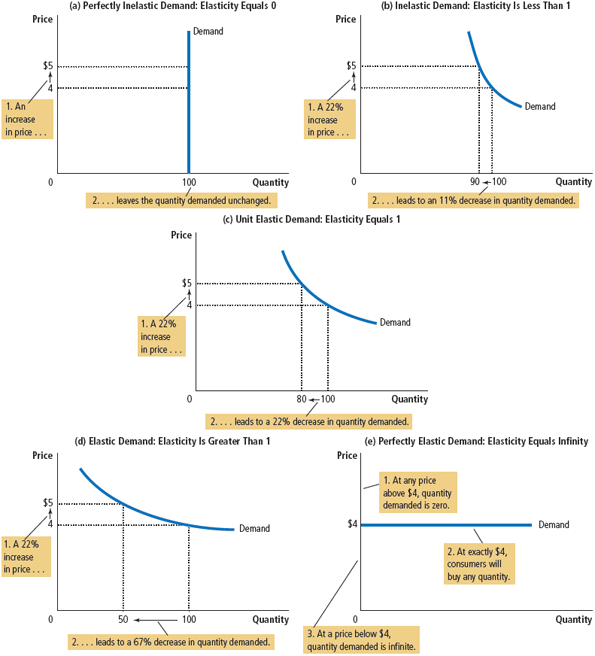
- 闭包: 在一些语言中,在函数中可以(嵌套)定义另一个函数时,如果内部的函数引用了外部的函数的变量,则可能产生闭包。闭包可以用来在一个函数与一组“私有”变量之间创建关联关系。在给定函数被多次调用的过程中,这些私有变量能够保持其持久性。
- 支持将函数当成对象使用的编程语言,一般都支持闭包。比如
Python,JavaScript。
闭包的示例
- 代码
1
2
3
4
5
6
7
8
9
10
11
12
13def function_1(arg_1):
def function_2(arg_2):
return arg_1 * arg_2
return function_2
times_8 = function_1(8)
out = times_8(9)
print(f"times_8(9) = {out}")
# 闭包中的 cell
print(f"times_8.__closure__ = {times_8.__closure__}")
# 闭包中的 cell 对象的内容
print("times_8.__closure__.cell_contents:")
for i in times_8.__closure__:
print(i.cell_contents) - 输出
1
2
3
4times_8(9) = 72
times_8.__closure__ = (<cell at 0x7ff39d4d2a30: int object at 0x5642a56c5e20>,)
times_8.__closure__.cell_contents:
8
闭包的用处
1. 可以读取函数内部的变量
- 如上面给出的例子
2. 让这些变量的值始终保持在内存中
- 例如一个棋盘游戏,棋子每次可以选择上下左右方向中的一个,在此方向上移动距离 step,使用闭包实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def create(pos=[0, 0]):
def go(direction, step):
new_x = pos[0] + direction[0] * step
new_y = pos[1] + direction[1] * step
pos[0] = new_x
pos[1] = new_y
return pos
return go
player = create()
print(player([1, 0], 10))
print(player([0, 1], 20))
print(player([-1, 0], 10)) - 输出
1
2
3[10, 0]
[10, 20]
[0, 20]
棋子每次更新后的位置都会存储在闭包中。
3. 用于装饰器
- 可以读取函数内部的变量 和 让这些变量的值始终保持在内存中 都可以使用
Python的类实现,但 装饰器 是闭包的一个典型用处。
装饰器 (Decorators)
装饰器的定义
- 装饰器: 由闭包的概念引申而来,是一种 增加函数或类功能的方法,它可以快速地给不同的函数或类传入相同的功能。
- 直白点说就是被装饰的函数或类,会作为参数传入到装饰器对应的函数或类中,在装饰器中会对传入的函数或类(被装饰的对象)进行一些处理,然后返回一个新的函数或类(通常是对原函数或类的增强版)。
函数装饰器的示例
- 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import time
def count_time(some_fun):
def wrapper():
t1 = time.time()
some_fun()
print(f"运行时间为: {round(time.time() - t1, 2)} s")
return wrapper
# 装饰器语法糖
def function_1():
time.sleep(1)
print("run function_1")
function_1()
# 不使用语法糖的方法
def function_2():
time.sleep(1)
print("run function_2")
new_function = count_time(function_2)
new_function() - 输出
1
2
3
4run function_1
运行时间为: 1.0 s
run function_2
运行时间为: 1.0 s
类别装饰器示例
- 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21import time
class Timer:
def __init__(self, func) -> None:
self.func = func
def __call__(self, *args, **kwargs):
start = time.time()
ret = self.func(*args, **kwargs)
print(f"Time: {time.time()-start}")
return ret
# 使用装饰器语法糖实现
def add_1(a, b):
time.sleep(1)
print(f"{a} + {b} = {a+b}")
add_1(2, 3)
# 不使用装饰器语法糖实现
def add_2(a, b):
time.sleep(1)
print(f"{a} + {b} = {a+b}")
new_add_2 = Timer(add_2)
new_add_2(2, 3) - 输出
1
2
3
42 + 3 = 5
Time: 1.0011768341064453
2 + 3 = 5
Time: 1.001098394393921