强化学习(2)——用Q Learning算法训练Agent玩Blackjack

URL

TL;DR

本文通过一个简单的例子介绍了如何用 Q Learning 算法训练一个 Agent 玩 Blackjack 游戏，环境是 OpenAI Gym 提供的 Blackjack-v0
Q Learning 算法是一种用于有限离散状态和动作环境下的强化学习算法，通过基于贝尔曼方程的更新策略，不断更新 Q Table 来学习最优策略，最终实现 Agent 的自动决策

Algorithm

Q Learning 算法

1. 环境介绍

Blackjack 游戏规则

graph TD
    A[开始] --> B[给玩家发两张牌，给庄家发两张牌，一张明牌，一张暗牌]
    
    B --> H{玩家是否有21点?}
    H -->|是| I[玩家有自然牌，检查庄家]
    H -->|否| N{玩家选择是否继续要牌?}
    
    I --> K{庄家是否也有自然牌?}
    K -->|是| L[平局]
    K -->|否| M[玩家胜利]
    
    N -->|要牌| O[发一张牌给玩家]
    N -->|停牌| P[玩家停牌，轮到庄家]
    
    O --> Q{玩家是否爆掉（超过21点）?}
    Q -->|是| R[玩家爆掉，庄家胜利]
    Q -->|否| N
    P --> S{庄家是否点数≥17?}
    S -->|是| T[庄家停牌]
    S -->|否| U[庄家要牌]
    
    U --> V{庄家是否爆掉?}
    V -->|是| M[玩家胜利]
    V -->|否| S
    
    T --> X{比较玩家和庄家的点数}
    X -->|玩家点数更大| M[玩家胜利]
    X -->|庄家点数更大| Z[庄家胜利]
    X -->|点数相同| L[平局]
    R --> AA[游戏结束]
    Z --> AA
    L --> AA
    M --> AA

Blackjack 环境定义：
- Observation space: Tuple(Discrete(32), Discrete(11), Discrete(2))，用一个三元组表示当前状态，分别是：
  - 玩家的点数
  - 庄家的明牌点数
  - 玩家是否有 Ace
- Action space: Discrete(2)
  - 0 表示 stick (停牌)
  - 1 表示 hit (要牌)
- Reward: +1 表示玩家胜利，-1 表示庄家胜利，0 表示平局
- Starting state:
  - 玩家牌之和为 4 - 21 之间
  - 庄家明牌为 1 - 10 之间
  - 玩家是否有 Ace 为 0 或 1
- Episode End:
  - 玩家停牌
  - 玩家爆牌

2. `Q Learning` 算法

特性	V 函数 (状态价值函数)	Q 函数 (状态-动作价值函数)
定义	评估状态 `s` 的价值，即在状态 `s` 开始，按照策略 `π` 执行的期望累积奖励	评估状态 `s` 和动作 `a` 的价值，即在状态 `s` 选择动作 `a`，然后按照策略 `π` 执行的期望累积奖励
输入	状态 `s`	状态 `s` 和动作 `a`
输出	状态的价值，即期望的回报	状态-动作对的价值，即从状态 `s` 执行动作 `a` 后的期望回报
更新方式	$V(s)$ 通过 $Q(s,a)$ 来更新，通常用贝尔曼方程	$Q(s,a)$ 直接通过贝尔曼方程更新，通常用于 `Q-learning` 或 `DQN`
公式	$V^\pi(s)=\mathbb E[\sum_{t=0}^{\infty}\gamma^tr_t\|s_0=s,\pi]$	$Q^\pi(s,a)=\mathbb E[\sum_{t=0}^{\infty}\gamma^tr_t\|s_0=s,a_0=a,\pi]$
主要用途	用于评估某一状态的好坏，特别适合评估策略	用于评估某一状态下选择特定动作的好坏，通常用于 `Q-learning` 等算法

Q Learning 算法是一种 Off-Policy 的强化学习算法，通过不断更新 Q Table 来学习最优策略
Q Table 是一个 State-Action 表，用于存储每个状态下每个动作的 Q Value，因此 Q Table 的大小是 Observation space length * Action space length
Q Value 的更新公式：

Q(s, a) = Q(s, a) + \alpha \cdot (r + \gamma \cdot \max_{a'} Q(s', a') - Q(s, a))

$Q(s, a)$ 是当前状态 s 下采取动作 a 的 Q Value
$\alpha$ 是学习率
$r$ 是当前状态下采取动作 a 后的奖励
$\gamma$ 是折扣因子，用于平衡当前奖励和未来奖励，越大表示越重视未来奖励，越小表示越重视当前奖励
$\max_{a'} Q(s', a')$ 是下一个状态 s' 下所有动作中最大的 Q Value

3. 使用 `Q Learning` 算法训练 `Agent` 玩 `Blackjack`

实现代码如下：

from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from matplotlib.patches import Patch
from tqdm import tqdm
from typing import Tuple
import gymnasium as gym
class BlackjackAgent:
    def __init__(
        self,
        env,
        learning_rate: float,
        initial_epsilon: float,
        epsilon_decay: float,
        final_epsilon: float,
        discount_factor: float = 0.95,
    ):
        """Initialize a Reinforcement Learning agent with an empty dictionary
        of state-action values (q_values), a learning rate and an epsilon.
        Args:
            learning_rate: The learning rate
            initial_epsilon: The initial epsilon value
            epsilon_decay: The decay for epsilon
            final_epsilon: The final epsilon value
            discount_factor: The discount factor for computing the Q-value
        """
        self.q_values = defaultdict(lambda: np.zeros(env.action_space.n))
        self.lr = learning_rate
        self.discount_factor = discount_factor
        self.epsilon = initial_epsilon
        self.epsilon_decay = epsilon_decay
        self.final_epsilon = final_epsilon
        self.training_error = []
    def get_action(self, env, obs: Tuple[int, int, bool]) -> int:
        """
        Returns the best action with probability (1 - epsilon)
        otherwise a random action with probability epsilon to ensure exploration.
        """
        # with probability epsilon return a random action to explore the environment
        if np.random.random() < self.epsilon:
            return env.action_space.sample()
        # with probability (1 - epsilon) act greedily (exploit)
        else:
            return int(np.argmax(self.q_values[obs]))
    def update(
        self,
        obs: Tuple[int, int, bool],
        action: int,
        reward: float,
        terminated: bool,
        next_obs: Tuple[int, int, bool],
    ):
        """Updates the Q-value of an action."""
        future_q_value = (not terminated) * np.max(self.q_values[next_obs])
        temporal_difference = (
            reward + self.discount_factor * future_q_value - self.q_values[obs][action]
        )
        self.q_values[obs][action] = (
            self.q_values[obs][action] + self.lr * temporal_difference
        )
        self.training_error.append(temporal_difference)
    def decay_epsilon(self):
        self.epsilon = max(self.final_epsilon, self.epsilon - self.epsilon_decay)
env = gym.make("Blackjack-v1", sab=True)
# hyperparameters
learning_rate = 0.01
n_episodes = 100_000
start_epsilon = 1.0
epsilon_decay = start_epsilon / (n_episodes / 2)  # reduce the exploration over time
final_epsilon = 0.1
agent = BlackjackAgent(
    env=env,
    learning_rate=learning_rate,
    initial_epsilon=start_epsilon,
    epsilon_decay=epsilon_decay,
    final_epsilon=final_epsilon,
)
env = gym.wrappers.RecordEpisodeStatistics(env, buffer_length=n_episodes)
for episode in tqdm(range(n_episodes)):
    obs, info = env.reset()
    done = False
    # play one episode
    while not done:
        action = agent.get_action(env, obs)
        next_obs, reward, terminated, truncated, info = env.step(action)
        # update the agent
        agent.update(obs, action, reward, terminated, next_obs)
        # update if the environment is done and the current obs
        done = terminated or truncated
        obs = next_obs
    agent.decay_epsilon()

代码中定义了一个 BlackjackAgent 类，用于实现 Q Learning 算法
初始化：
1. 初始化 Q Table 为一个空的字典，Q Value 为 0
2. 学习率为 0.01
3. 折扣因子为 0.95
4. 初始 epsilon 为 1.0，随着训练逐渐减小为 0.1
get_action 方法用于根据当前状态选择动作，以 epsilon 的概率选择随机动作，以 1 - epsilon 的概率选择最优动作
update 方法用于更新 Q Value，根据 Q Learning 公式更新 Q Value

4. 训练结果

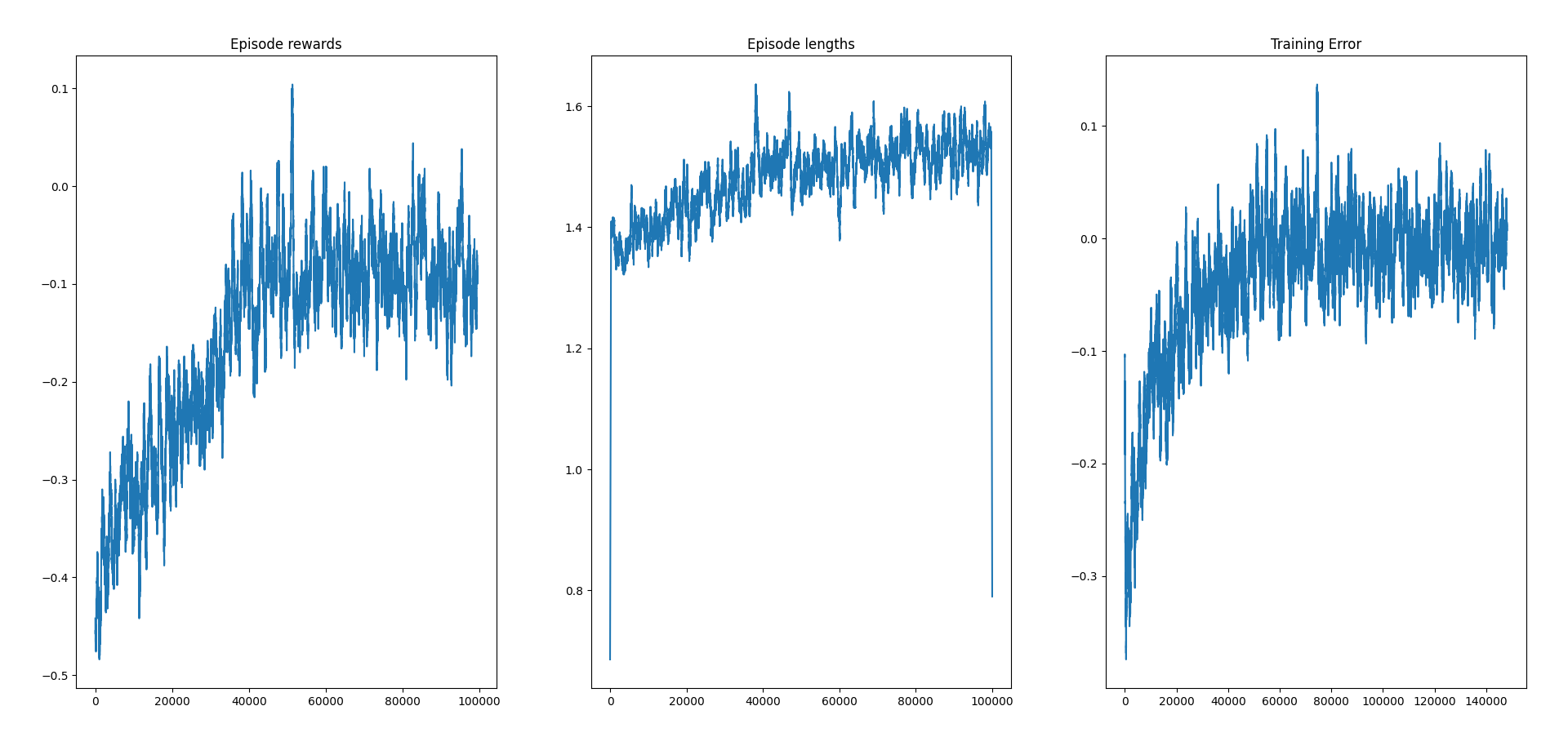
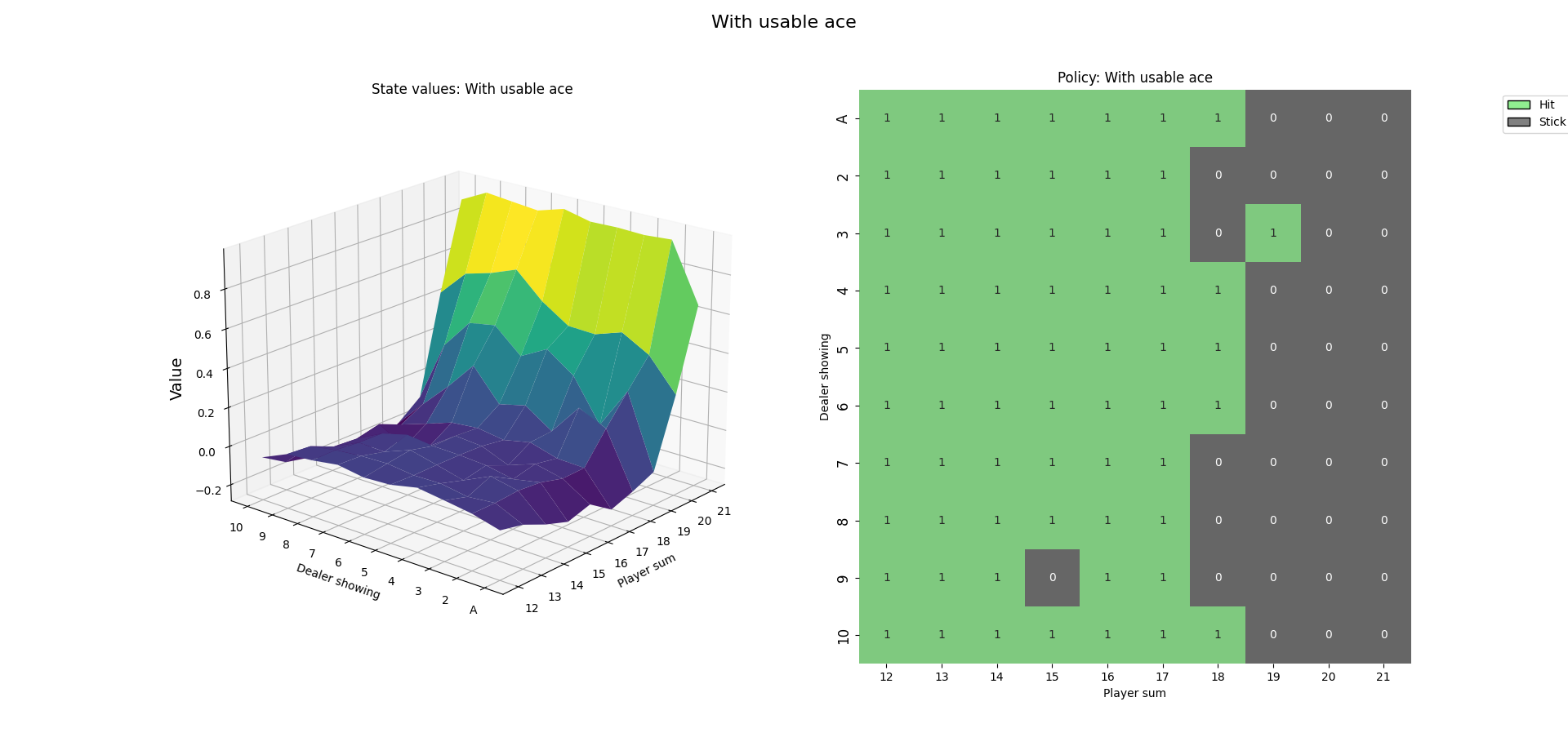
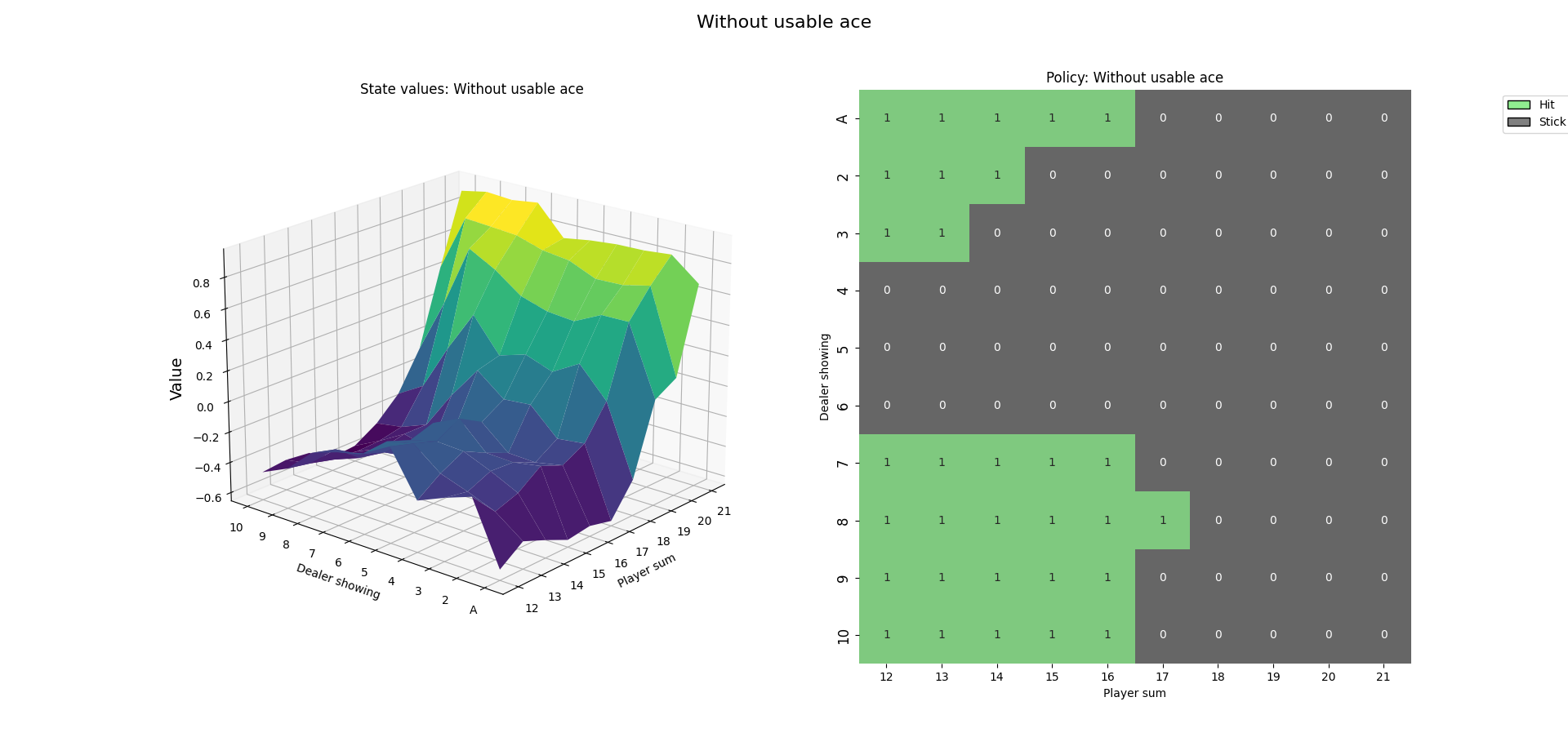
Thoughts

Q Learning 算法的关键是更新 Q Table 的过程，原理是贝尔曼方程： $Q(s,a)=\mathbb E[R_{t+1}+\gamma\ max_{a'}Q(s_{t+1},a')|S_t=s,A_t=a]$ ，表示当前状态下采取动作 a 的 Q Value 等于即时奖励加上折扣后未来（下一个时间步）状态的最大 Q Value
对于 State Space 和 Action Space 比较大的问题，Q Learning 算法的 Q Table 可能会非常庞大，因此需要使用 Deep Q Learning 算法，用神经网络来近似 Q Value，以减少存储空间，也就是 DQN 算法

URL

TL;DR

Algorithm

1. 环境介绍

2. Q Learning 算法

3. 使用 Q Learning 算法训练 Agent 玩 Blackjack

4. 训练结果

Thoughts

2. `Q Learning` 算法

3. 使用 `Q Learning` 算法训练 `Agent` 玩 `Blackjack`