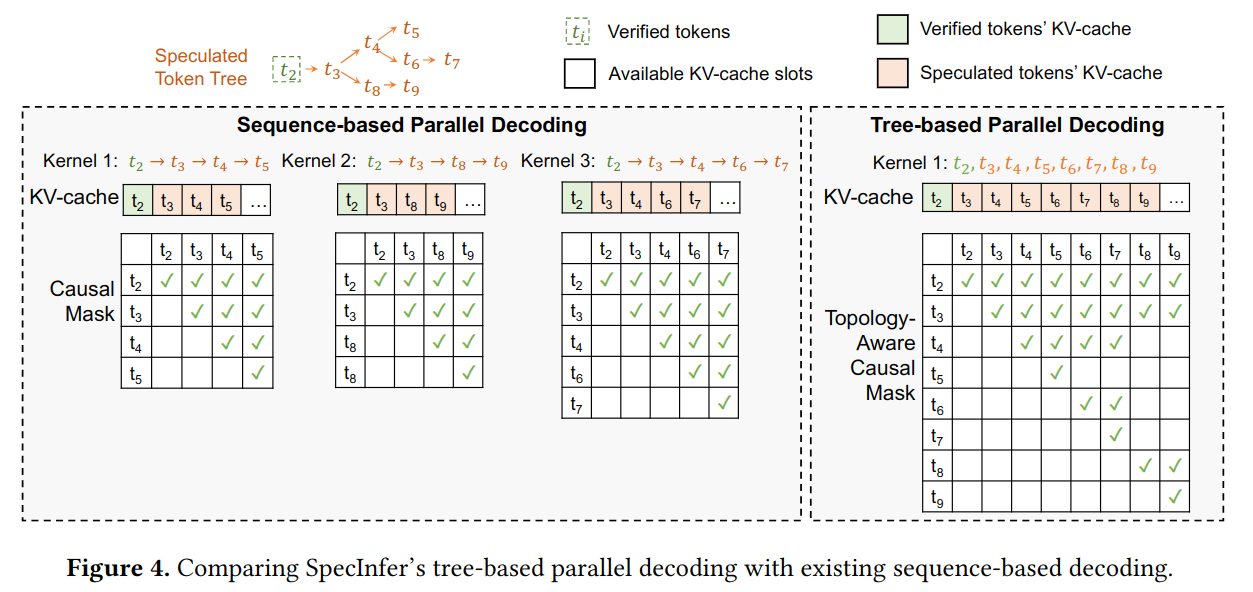
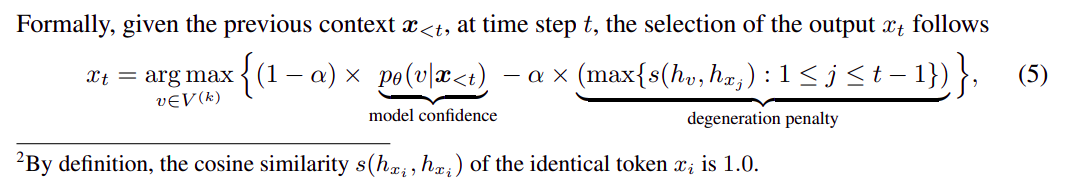Zhangzhe's Blog

The projection of my life.

0%

Posted on Edited on In Valine:

URL

TL;DR

  • 本文提出一种和 Gpipe 类似的 pipeline parallelism 并行训练机制 PipeDream，和 Gpipe 可以任意划分模型不同，PipeDream 自动化划分网络，以实现负载均衡和最小通信开销。
  • 与 Gpipe 的同步更新机制不同，PipeDream 采用异步参数更新机制。

Algorithm

PipeDream_1.png

backward 的过程实际同时包含了 参数更新

  • 与 Gpipe 使用的 Micro-Batch + 同步参数更新机制不同，PipeDream 使用异步更新机制，异步更新主要包含以下几点：

weigt stashing

  1. 从上图可以看出 Machine 1 在 forward 5 时，使用的是更新过 1 次的参数（forward 5 之前只做了 backward 1）；但当 backward 5 时，参数已经被更新了 4 次，如果直接使用会出现 forward 和 backward 参数不一致问题
  2. 因此，PipeDream 提出了 weight stashing (权重存储)，即保存多组 weights，每次 forward 过程使用最新版本的 weights，当 backward 时，使用 forward 时刻对应的 weights
  3. 使用 weight stashing 之前，w(t+1)=w(t)+γ⋅△f(w1(t),w2(t),...,wn(t))w^{(t+1)} = w^{(t)}+\gamma \cdot \triangle f(w_1^{(t)},w_2^{(t)},...,w_n^{(t)})，其中：
    1. γ\gamma 表示 learning rate
    2. nn 表示 stage 的数量，即 GPU 数量
    3. wi(t)w_i^{(t)} 表示 weights of stage i after t mini-batch，即当运行了 t 个 mini-batch 之后的 stage i 的权重
    4. △f\triangle f 表示梯度
  4. 使用 weight stashing 之后，w(t+1)=w(t)+γ⋅△f(w1(t−n+1),w2(t−n+2),...,wn(t))w^{(t+1)} = w^{(t)}+\gamma \cdot \triangle f(w_1^{(t-n+1)},w_2^{(t-n+2)},...,w_n^{(t)})

vertical sync

  1. weight stashing 解决了 forward 和 backward 使用的 weight 版本不一致问题，但依然存在另外一个问题：同一个 mini-batch 在不同 stage 上 forward 使用的 weight 版本不一致
  2. 例如，对于 mini-batch 4，在 Machine 2 上 forward 使用的参数版本是未更新版本，在 Machine 3 上 forward 使用的版本是更新过一次的版本
  3. 为解决这个问题，作者提出 vertical sync 概念，即：对于一个 mini-batch 在每个 stage 上 forward 都使用最旧版本的参数，stage forward and backward 结束后统一更新参数
  4. vertical sync 应用之后，w(t+1)=w(t)+γ△f(w1(t−n+1),w2(t−n+1),...,wn(t−n+1))w^{(t+1)}=w^{(t)}+\gamma \triangle f(w_1^{(t-n+1)},w_2^{(t-n+1)},...,w_n^{(t-n+1)})
  5. 事实上实验证明，weight stashing 对训练精度提升明显，vertical sync 提升较小

Thought

  • 感觉 PipeDream 为了充分排流水，减小 bubble，没有等 forward 全部结束就开始 backward，然后发现和单 GPU 更新机制不等价，然后用了 weight stashing 和 vertical sync 去找补，做到等价
  • 和 Gpipe 相比，灵活性更差，实现难度更高（需要缓存各个版本的 weights，听上去也是几倍的存储开销以及吞吐量）

Posted on Edited on In Valine:

URL

TL;DR

  • 随着模型和数据量的增长，单 GPU 已经无法满足需求，所以需要多 GPU 并行
  • Data parallelism 是最常用的，即将数据划分到多个 GPU 上，每个 GPU 单独前向反向传播，仅在梯度更新时聚合，例如 pytorch ddp
  • 本论文提出一种新的并行方式 Pipeline parallelism，这种方式是将模型划分为多段子图，每个设备上加载一段，各个子图直接串联
  • 直接实现的 Pipeline parallelism 的 GPU 利用率较低，本文通过一些方法可大幅提高 GPU 利用率

Algorithm

gpipe_1.png
Gpipe 方案主要包含三个部分

划分 Stage

  1. 模型切成若干 stage，每个 GPU 只加载一段
  2. 每个 stage 串起来形成一个 pipeline

划分 Micro-Batch

  1. 传统模型训练过程中使用 Mini-Batch，Mini-Batch 在 pipeline parallelism 中会出现大量气泡，因此 Gpipe 提出 Micro-Batch 概念
  2. Micro-Batch 是将 Mini-Batch 再划分成多份，用于排计算流水，Micro-Batch 变成最小计算单元，有利于减小气泡，上图 2.c 中横向就是一个 Mini-Batch 划分得到的一组 Micro-Batch
  3. 为了保证梯度更新和 Mini-Batch 的一致性，Gpipe 会将 Micro-Batch 梯度累积，在一个 Mini-Batch 的全部 Micro-Batch 计算结束后再更新（图 2.c 中一行只有一次 update）

重计算

  1. 传统模型训练过程中，计算的中间结果都需要保存，用于反向传播计算梯度，非常消耗显存，同时会导致 pipeline parallelism 的数据依赖问题，上图 2.a 中的横向连接
  2. 重计算是一种用计算换空间的操作，在前向传播过程中，丢弃 stage 内所有中间结果，只保留 stage 间中间结果；在反向传播时，stage 内中间结果会再做一次前向传播计算得到
  3. 重计算可大幅降低显存占用，使得可以放更大的 batch size 和更大的模型，且可以改善数据依赖问题

Thought

  • 这种方案前瞻性比较强，提出时还没有 LLM，且拥有和传统非并行训练在数学上一致的参数更新机制
  • 给并行训练提供了一种新思路，非常灵活

Posted on Edited on In Valine:

URL

TL;DR

  • 本文利用了 Speculative decoding 思想实现了一个 SpecInfer 大语言模型推理加速系统
  • 和标准 Speculative decoding 使用 seq 组织预测的 token 不同，SpecInfer 使用 tree 数据结构组织预测的 token
  • SpecInfer 中的 target 模型可以并行验证整个 token tree 的正确性，而不是 token seq，且可以保证和原模型输出完全一致

Algorithm

增量式解码、序列式投机解码、树式投机解码三者对比

specinfer_1.png

左图表示传统增量式推理 LLM 的解码方式
右图从上到下依次表示：增量式解码、序列式投机解码、树式投机解码

候选树生成和验证流程

specinfer_2.png

SSM (small speculative model) 给出候选树
target model 对候选树进行验证

如何对树式结构并行解码

specinfer_3.png

注意：这的 “并行” 是指可以一次解码一棵树而不需要将树深度优先搜索得到多组序列然后一一解码

  1. 使用 kv cache 对解码过程进行加速是一个常见的方法，但树式结构无法直接使用 kv cache（因为要动态剪枝，如图左侧所示）
  2. 因此本文提出一种新颖的方法使得树式结构可以并行解码，这个方法包括两个改进：
    1. 对树进行 深度优先搜索，使得树变成一个序列
    2. 将传统的上三角 attention mask 变成一个 topology-aware mask，即通过 mask 来确定 token 两两之间的可见性（如图右侧所示），这种可见性包含：
      1. 每个 token 看不到之后的 token（矩阵下三角置 −∞-\infty）
      2. 每个 token 看不到不在其拓扑路径上的 token

总体算法流程

specinfer_4.png

  1. 先用 small speculate model 推理 sequence 得到候选树 NN
  2. 在使用 LLM 树式并行解码 sequence 得到大模型预测结果 OO
  3. 用贪心算法或随机匹配算法对候选树 NN 逐个节点验证（接受或拒绝）
  4. 重复直到 <EOS> 出现

贪心验证算法和随机验证算法

specinfer_5.png

贪心验证

  1. uu 表示当前节点，从根节点开始广度优先遍历
  2. pv=up_v=u 表示 vv 是 uu 的子节点
  3. tv=O(u)t_v=O(u) 表示大模型和投机模型预测结果一致

随机验证

  1. uu 表示当前节点，从根节点开始广度优先遍历
  2. 当在 [0, 1] 之间随机均匀采样得到的随机数 r<PLLMPSSMr \lt \frac{P_{LLM}}{P_{SSM}} 时，接受这个节点，否则拒绝

Thought

  • 这篇论文站在 speculate decoding 的肩膀上，加入了树结构的候选列表，算是 speculate decoding 的超集
  • topology-aware mask 和 decoder attention mask 结合的方法还是挺巧妙的
  • 由于是树结构存储候选词，那么多个 SSM 是天然适配的，算是个工程角度很好用的 trick

Posted on Edited on In Valine:

URL

TL;DR

  • 本文提出一种新颖的大模型推理加速的新范式，叫做投机解码，用一个参数量很小的近似模型预测得到一段序列，让大模型评判 接受 还是 拒绝 这段序列。
  • 从数学上可以证明投机解码的结果和大模型逐个 token 预测的结果完全相同。
  • 可以加速推理 2 - 3 倍，据说 GPT-4 使用了这种方法。
  • 近似小模型的参数量一般要比大模型小 2 个数量级。
    E(generated tokens)=1−βγ+11−βE(\textit{generated tokens}) = \frac{1-\beta^{\gamma+1}}{1-\beta}

Algorithm

算法流程

  1. 给定 prefix_seq 序列，用近似小模型（approx model， M_q）预测 γ\gamma 长度的后续序列，记做 predict_seq，并记录 predict_seq 中每一个 token 的预测概率，记作 q
  2. 大模型（target model，M_p）输入 prefix_seq + predict_seq，得到 predict_seq 每个 token 的概率（记作 p）和下一个 token（记作 t）
  3. 对于每一个 token，如果 p >= q，则表示大模型接受小模型对这个 token 的提议；如果 p < q，则表示 大模型以 pq\frac{p}{q} 的概率接受这个 token，用随机均匀采样来确定是否接受这个 token
  4. 添加大模型连续接受的 predict_seq 到 prefix_seq 之后，如果 predict_seq 每个 token 都接受了，则 prefix_seq = prefix_seq + predict_seq + t。重复步骤 1

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
@torch.no_grad()
def speculative_sampling(
    prefix: torch.Tensor,
    approx_model: torch.nn.Module,
    target_model: torch.nn.Module,
    max_len: int,
    gamma: int = 4,
    temperature: float = 1,
    top_k: int = 0,
    top_p: float = 0,
) -> torch.Tensor:
    seq_len = prefix.shape[1]
    T = seq_len + max_len
    approx_model_cache = KVCacheModel(approx_model, temperature, top_k, top_p)
    target_model_cache = KVCacheModel(target_model, temperature, top_k, top_p)
    resample_count = 0
    target_sample_count = 0
    accepted_count = 0
    while prefix.shape[1] < T:
        prefix_len = prefix.shape[1]
        x = approx_model_cache.generate(prefix, gamma)
        _ = target_model_cache.generate(x, 1)
        n = prefix_len + gamma - 1
        for i in range(gamma):
            r = torch.rand(1, device=target_model_cache.device)
            j = x[:, prefix_len + i]
            if r > (target_model_cache._prob_history[:, prefix_len + i - 1, j]) / (
                approx_model_cache._prob_history[:, prefix_len + i - 1, j]
            ):
                # reject
                n = prefix_len + i - 1
                break
            accepted_count += 1
        prefix = x[:, : n + 1]
        approx_model_cache.rollback(n + 1)
        if n < prefix_len + gamma - 1:
            # reject someone, sample from the pos n
            t = sample(
                max_fn(
                    target_model_cache._prob_history[:, n, :]
                    - approx_model_cache._prob_history[:, n, :]
                )
            )
            resample_count += 1
            target_model_cache.rollback(n + 1)
        else:
            # all approx model decoding accepted
            assert n == target_model_cache._prob_history.shape[1] - 1
            t = sample(target_model_cache._prob_history[:, -1, :])
            target_sample_count += 1
        prefix = torch.cat((prefix, t), dim=1)
    return prefix

收益分析

  • 大模型推理过程中，预填充阶段计算访存比较高，增量生成阶段计算访存比较低，因此增量生成阶段是主要优化方向
  • 本论文的投机解码算法在某种程度上是将 target model 的增量生成阶段变成 approx model 的增量生成 + target model 的预填充，收益主要来自于这里
  • 且投机解码算法和其他大模型推理算法（例如 kv cache、flash attention、MQA / GQA）并不冲突，可以合并使用达到最优加速效果

Thought

  • 从另外一种新颖且符合逻辑的方面优化了大模型推理

Posted on Edited on In Valine:

URL

TL;DR

  • 本文提出来一种 Typical sampling 的解码策略，是对 top-p sampling 的改进，启发了后续的 η−sampling\eta-sampling 解码策略，旨在生成更自然、更符合人类语言使用习惯的文本。
  • 论文使用信息论的观点，局部典型性（local typicality）采样的依据是条件熵和信息量的接近程度
    • 条件熵：(−log(p)∗p).sum()(-log(p)*p).sum()
    • 信息量：−log(p)-log(p)

Algorithm

公式角度理解

  • 在时间步 tt，候选词集合为：

Lϵ(T)={y=y0,...,yT∣∀1≤t≤T,∣log⁡p(yt∣y<t)+H(Yt∣Y<t=y<t)∣<ϵ}L_{\epsilon}^{(T)}=\{y=y_0,...,y_T| \forall 1\le t \le T, | \log p(y_t|y_{\lt t}) + H(Y_t|Y_{\lt t=y \lt t}) | \lt \epsilon \}

  • 其中
    • ∣log⁡p(yt∣y<t)+H(Yt∣Y<t=y<t)∣<ϵ| \log p(y_t|y_{\lt t}) + H(Y_t|Y_{\lt t=y \lt t}) | \lt \epsilon 表示信息量和条件熵最大相差不大于 ϵ\epsilon，写成 ∣H(Yt∣Y<t=y<t)−(−log⁡p(yt∣y<t))∣<ϵ|H(Y_t|Y_{\lt t=y \lt t}) - (-\log p(y_t|y_{\lt t}) ) | \lt \epsilon 更容易理解
    • ϵ\epsilon 是超参数，需要在 (0, 1) 之间

代码角度理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class TypicalLogitsWarper(LogitsWarper):
    def __init__(self, mass: float = 0.9, filter_value: float = -float("Inf"), min_tokens_to_keep: int = 1):
        mass = float(mass)
        if not (mass > 0 and mass < 1):
            raise ValueError(f"`typical_p` has to be a float > 0 and < 1, but is {mass}")
        if not isinstance(min_tokens_to_keep, int) or (min_tokens_to_keep < 1):
            raise ValueError(f"`min_tokens_to_keep` has to be a positive integer, but is {min_tokens_to_keep}")
        self.filter_value = filter_value
        self.mass = mass
        self.min_tokens_to_keep = min_tokens_to_keep
    def __call__(self, input_ids: torch.LongTensor, scores: torch.FloatTensor) -> torch.FloatTensor:
        # calculate entropy
        normalized = torch.nn.functional.log_softmax(scores, dim=-1)
        p = torch.exp(normalized)
        ent = -(normalized * p).nansum(-1, keepdim=True)
        # shift and sort
        shifted_scores = torch.abs((-normalized) - ent)
        sorted_scores, sorted_indices = torch.sort(shifted_scores, descending=False)
        sorted_logits = scores.gather(-1, sorted_indices)
        cumulative_probs = sorted_logits.softmax(dim=-1).cumsum(dim=-1)
        # Remove tokens with cumulative mass above the threshold
        last_ind = (cumulative_probs < self.mass).sum(dim=1)
        last_ind.clamp_(max=sorted_scores.shape[-1] - 1)
        sorted_indices_to_remove = sorted_scores > sorted_scores.gather(1, last_ind.view(-1, 1))
        sorted_indices_to_remove[..., : self.min_tokens_to_keep] = 0
        indices_to_remove = sorted_indices_to_remove.scatter(1, sorted_indices, sorted_indices_to_remove)
        scores_processed = scores.masked_fill(indices_to_remove, self.filter_value)
        return scores_processed

Thought

  • 单看计算过程实际上比较符合直觉，用信息论的角度理解反而会云里雾里…

Posted on Edited on In Valine:

URL

TL;DR

  • 常用的 top-p random sampling decoding method 可能会导致输出的长文本质量较差
  • 本文设计了一种基于熵的动态概率阈值优化 top-p 随机采样算法，叫做 η−sampling\eta-sampling

Algorithm

公式表示

Ax<i={x∈V∣Pθ(x∣x<i)>η}A_{x \lt i}=\{x \in V | P_{\theta}(x | x \lt i) \gt \eta \}

η=min(ϵ,α(−hη,x<i))\eta=min(\epsilon,\alpha(-h_{\eta,x<i}))

其中第一行公式表示随机采样概率值截断到 η\eta
第二行中 ϵ,α\epsilon,\alpha 是超参数，通常 α=ϵ\alpha=\sqrt{\epsilon}，h 表示输出的熵，h=−(p∗log(p)).sum()h=-(p*log(p)).sum()，p 表示概率

代码表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class EtaWarper(transformers.LogitsWarper):
  """Our proposed eta sampling warper."""
  def __init__(self, epsilon):
    self.epsilon = epsilon
    self.filter_value = -float("Inf")
  def __call__(self, input_ids, scores) -> torch.FloatTensor:
    probabilities = scores.softmax(dim=-1)
    entropy = - (probabilities * torch.log(probabilities)).sum()
    eta = min(self.epsilon, torch.sqrt(torch.tensor(self.epsilon))*torch.exp(-entropy))
    indices_to_remove = probabilities < eta
    max_word = torch.argmax(scores,dim=-1)
    # 防止把候选词全删了，至少留一个
    indices_to_remove[...,max_word.squeeze()] = 0
    new_scores = scores.masked_fill(indices_to_remove, self.filter_value)
    return new_scores

Thought

  • 是 top-p 的小升级，计算量较小，算是一个小 trick

Posted on Edited on In Valine:

URL

TL;DR

  • 本文提出一种叫做 Contrastive search 的解码方法，比 top-k / top-p 等随机解码方法和 argmax 这种贪心解码方法更优，模型输出内容语意更连贯，模型更不容易退化
  • Contrastive search 是在 top-k 基础上增加了 degeneration penalty（退化惩罚项），算是 random sampling 类算法的升级版
  • 但需要将候选的 top-k 输出追加到序列末尾作为输入重新输入到模型中输出 top-k 对应的 hidden state，因此时间复杂度较高

Algorithm

总体架构

contrastive_search_1.png

其中 α\alpha 是超参数，用来平衡模型预测结果和退化惩罚项
h 表示 hidden state，用 hvh_v 和序列中每一个 token 的 hidden state 计算相似度
由于 hvh_v 只能在下一次 inference 时产生，所以需要在 decoding 阶段再推理一次，这一步比较麻烦

用一段代码来描述一下解码过程

  1. 首先在 t-1 时刻输入 seq_len 长度的序列，输出 vocab_size 长度的 logits，选 top-k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# compute the logits in this step
prev_hidden_states, logits = model.compute_logits_and_hidden_states(input_ids)
_, seqlen, embed_dim = prev_hidden_states.size()
_, _, vocab_size = logits.size()
logit_for_next_step = logits[:,-1,:]
assert logit_for_next_step.size() == torch.Size([1, vocab_size])
# normalize with the softmax function
next_probs = F.softmax(logit_for_next_step, dim = -1)
assert next_probs.size() == logit_for_next_step.size()
# collecte top-k candidate tokens and their logits (model confidence)
_, next_top_k_ids = torch.topk(logit_for_next_step, dim = -1, k = beam_width)
assert next_top_k_ids.size() == torch.Size([1, beam_width])
        
next_top_k_probs = torch.gather(next_probs, dim = 1, index=next_top_k_ids)
assert next_top_k_probs.size() == next_top_k_ids.size()
  1. 将 top-k 预测的每一种可能追加到原始序列，并在 batch size 维度 concat 成一个 shape = [beam_width, seq_len + 1, dim] 的输入
1
2
3
4
5
6
7
# concatenate each candidate token with prefix
expanded_context = [input_ids for _ in range(beam_width)]
expanded_context = torch.cat(expanded_context, dim = 0)
assert expanded_context.size() == torch.Size([beam_width, seqlen])
top_k_ids = top_k_ids.view(beam_width, 1)
next_input_ids = torch.cat([expanded_context, top_k_ids], dim = -1)
assert next_input_ids.size() == torch.Size([beam_width, seqlen+1])
  1. 将 shape = [beam_width, seq_len + 1, dim] 输入到模型中，计算得到每个 token 的 hidden state
1
2
3
4
5
6
7
# feed these candidates into next round to get their hidden states
new_hidden_states, next_logits = model.compute_logits_and_hidden_states(next_input_ids)
assert new_hidden_states.size() == torch.Size([beam_width, seqlen+1, embed_dim])
context_hidden = new_hidden_states[:,:seqlen,:]
assert context_hidden.size() == torch.Size([beam_width, seqlen, embed_dim])
next_hidden = new_hidden_states[:,seqlen:,:]
assert next_hidden.size() == torch.Size([beam_width, 1, embed_dim])
  1. 计算每一个 next hidden state 和 context hidden state 之间的相关性，相关性越高，说明重复性越高，惩罚越重，选择此 token 作为 next input id 的可能性越低
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def ranking(context_hidden, next_hidden, next_top_k_ids, next_top_k_probs, alpha):
    '''
        context_hidden: beam_width x context_len x embed_dim
        next_hidden: beam_width x 1 x embed_dim
        next_top_k_ids: beam_width x 1
    '''
    beam_width, context_len, embed_dim = context_hidden.size()
    assert next_hidden.size() == torch.Size([beam_width, 1, embed_dim])
    norm_context_hidden = context_hidden / context_hidden.norm(dim=2, keepdim=True)
    norm_next_hidden = next_hidden / next_hidden.norm(dim=2, keepdim=True)
    cosine_matrix = torch.matmul(norm_context_hidden, norm_next_hidden.transpose(1,2)).squeeze(-1)
    assert cosine_matrix.size() == torch.Size([beam_width, context_len])
    scores, _ = torch.max(cosine_matrix, dim = -1)
    assert scores.size() == torch.Size([beam_width])
    next_top_k_probs = next_top_k_probs.view(-1)
    scores = (1.0 - alpha) * next_top_k_probs - alpha * scores 
    _, selected_idx = torch.topk(scores, k = 1)
    assert selected_idx.size() == torch.Size([1])
    selected_idx = selected_idx.unsqueeze(0)
    assert selected_idx.size() == torch.Size([1,1])
    next_id = torch.gather(next_top_k_ids, dim = 0, index=selected_idx)
    assert next_id.size() == torch.Size([1,1])
    return next_id

Thought

  • 道理上讲得通，但多推理的一次是实实在在的计算代价，总计算量直接翻倍，真的会有大模型选择这种解码方式吗？

Posted on Edited on In Valine:

URL

TL;DR

  • 本文提出一种比 T5 bias 更简单的 position embedding 方法叫做 ALiBi (Attention with Linear Bias)，简单好用
  • 可以在短数据集上训练，在长数据集上测试，即具有外推性

Algorithm

T5 bias

  • 先讲一下 T5 bias 是如何实现 position embedding 的，主要分三步：
    1. 计算 query / key 的 n * n 相对位置矩阵，形如： 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      [[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [-1,  0,  1,  2,  3,  4,  5,  6,  7,  8],
       [-2, -1,  0,  1,  2,  3,  4,  5,  6,  7],
       [-3, -2, -1,  0,  1,  2,  3,  4,  5,  6],
       [-4, -3, -2, -1,  0,  1,  2,  3,  4,  5],
       [-5, -4, -3, -2, -1,  0,  1,  2,  3,  4],
       [-6, -5, -4, -3, -2, -1,  0,  1,  2,  3],
       [-7, -6, -5, -4, -3, -2, -1,  0,  1,  2],
       [-8, -7, -6, -5, -4, -3, -2, -1,  0,  1],
       [-9, -8, -7, -6, -5, -4, -3, -2, -1,  0]]
    2. 将相对位置矩阵分桶（超过 num_buckets 的饱和到 num_buckets） 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      [[ 0, 17, 18, 19, 20, 21, 22, 23, 24, 24],
       [ 1,  0, 17, 18, 19, 20, 21, 22, 23, 24],
       [ 2,  1,  0, 17, 18, 19, 20, 21, 22, 23],
       [ 3,  2,  1,  0, 17, 18, 19, 20, 21, 22],
       [ 4,  3,  2,  1,  0, 17, 18, 19, 20, 21],
       [ 5,  4,  3,  2,  1,  0, 17, 18, 19, 20],
       [ 6,  5,  4,  3,  2,  1,  0, 17, 18, 19],
       [ 7,  6,  5,  4,  3,  2,  1,  0, 17, 18],
       [ 8,  7,  6,  5,  4,  3,  2,  1,  0, 17],
       [ 8,  8,  7,  6,  5,  4,  3,  2,  1,  0]]

      这里上三角和下三角都有值是因为 encoder bidirection=True，如果是 decoder，则如下：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [2, 1, 0, 0, 0, 0, 0, 0, 0, 0],
       [3, 2, 1, 0, 0, 0, 0, 0, 0, 0],
       [4, 3, 2, 1, 0, 0, 0, 0, 0, 0],
       [5, 4, 3, 2, 1, 0, 0, 0, 0, 0],
       [6, 5, 4, 3, 2, 1, 0, 0, 0, 0],
       [7, 6, 5, 4, 3, 2, 1, 0, 0, 0],
       [8, 7, 6, 5, 4, 3, 2, 1, 0, 0],
       [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]]
    3. 最后是将此 n * n 的 relative position bucket 通过可学习的 embedding 函数变成 n * n * num_heads 的向量，和每个头的 attention score（softmax 之前） 相加，然后通过逐行 softmax 得到 attention weight

ALiBi

alibi_1.png

  • 用数学公式表示：softmax(qiKT+m⋅[−(i−1),...,−2,−1,0])softmax(q_iK^T+m\cdot[-(i-1),...,-2,-1,0])
  • ALiBi 的计算和 T5 bias 的前两步几乎一模一样
  • 第三步不再使用可学习的 embedding 函数映射到每个头上，而是将距离矩阵的值和每个头独立的 不可学习的 常量 m 值相乘，然后和 attention score 相加
  • mh=b(2(8/H)⋅b)hm_h = \frac{b}{(2^{(8/H)} \cdot b)^h}
    • b 是一个基数
    • H 是注意力头的数量
    • h 是注意力头的索引（从 0 到 H-1）

Thought

  • 标准 attention 的 pe∈Rn×dpe \in \mathbb{R}^{n\times d} 已经慢慢被淘汰了，不管是 RoPE / T5 Bias / ALiBi 都已经逐渐演变成 pe∈Rn×npe \in \mathbb{R}^{n\times n} 直接作用在 attention score 上了
  • ALiBi 的外推性其实本质是强行饱和掉远距离，有点过于粗暴了…

Posted on Edited on In Valine:

URL

TL;DR

  • GPT like 大语言模型目前在生成式大模型领域占了主导地位，这些模型每一次推理只得到一个 token，下一次推理会将得到的 token 放到上一次输入 token 序列的末尾作为新输入，直到达到 max_seq_length 或输出的 token 表示 end of sequence
  • 这种 GPT like 的生成机制意味着每次推理需要将之前所有 token 再重复算一次，序列长度越长，计算量越大，耗时越长
  • KV Cache 通过缓存上一次推理过程中每一层 transformer 的 key / value，将推理的时间复杂度从 O(n2)\mathcal{O}(n^2) 降低到了 O(n)\mathcal{O}(n)，且计算结果完全等价

Algorithm

  • 可以在本时间步使用上一个时间步缓存的 key / value 的必要理论依据是：
    1. 每个时间步输入的 token 序列除最后一个 token 之外都和上一个时间步输入相同
    2. attention mask 是下三角矩阵
    3. 对 attention score 矩阵做 softmax 是逐行的而不是全局的或逐列的
    4. 除 self-attention 操作之外，GPT like LLM 的其他层（layer norm, gelu, FFN 等）对 seq_len 维度来说都是 element-wise 的，且在推理阶段是静态的
  • 以上四个理论依据在 GPT like 模型中都满足，下面解释四个条件为什么是必不可少的：
    1. 如果上面第一个条件不满足，那么每次推理都是新的内容，缓存将毫无意义
    2. 下三角矩阵和逐行做 softmax 是必不可少的，随着 token 长度加一，每一层的 attention score 矩阵都会在最右和最下分别加一列和一行，由于下三角的存在，除最后一行外，其他每一行的值都不会改变（新加的一列不参与计算），而且逐行做，新加的一列也不影响其他行
    3. self-attention 是 GPT like LLM 中唯一一个在 token feature 间做信息融合的算子，其他算子都是在 token feature 内做且都是静态操作，所以随着序列长度变长，之前的序列特征都是静态的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
import torch
import torch.nn as nn
class SelfAttention(nn.Module):
    def __init__(self, dim, layer_idx):
        super(SelfAttention, self).__init__()
        self.dim = dim
        self.layer_idx = layer_idx
        self.query = nn.Linear(dim, dim)
        self.key = nn.Linear(dim, dim)
        self.value = nn.Linear(dim, dim)
        self.softmax = nn.Softmax(dim=-1)  # 重点是这里，逐行进行 softmax，而不是全局
        self.dropout = nn.Dropout(0.1)
        self.layer_norm = nn.LayerNorm(dim)
    def forward(self, x, attn_mask=None):
        q = self.query(x)
        k = self.key(x)
        v = self.value(x)
        scores = torch.matmul(q, k.transpose(-2, -1))
        scores = scores / torch.sqrt(torch.tensor(self.dim).float())
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask == 0, float("-inf"))
        attention_weights = self.softmax(scores)
        attention_weights = self.dropout(attention_weights)
        print("layer_idx:", self.layer_idx)
        print("q.sum(-1) =", q.squeeze().abs().sum(-1).tolist())
        print("k.sum(-1) =", k.squeeze().abs().sum(-1).tolist())
        print("v.sum(-1) =", v.squeeze().abs().sum(-1).tolist())
        print("attention_weights =\n", attention_weights.squeeze())
        print("#" * 100)
        output = torch.matmul(attention_weights, v)
        output = self.layer_norm(output + x)
        return output
class GPTModel(nn.Module):
    def __init__(self, dim, num_layers):
        super(GPTModel, self).__init__()
        self.dim = dim
        self.num_layers = num_layers
        self.attentions = nn.ModuleList(
            [SelfAttention(dim, i) for i in range(num_layers)]
        )
        self.linear1 = nn.Linear(dim, dim)
        self.linear2 = nn.Linear(dim, dim)
        self.dropout = nn.Dropout(0.1)
        self.layer_norm = nn.LayerNorm(dim)
    def forward(self, x, attn_mask=None):
        for i in range(self.num_layers):
            x = x + self.attentions[i](x, attn_mask=attn_mask)
            x = self.layer_norm(x)
            x = x + self.linear2(self.dropout(torch.relu(self.linear1(x))))
            x = self.layer_norm(x)
        return x
# Example usage
model = GPTModel(dim=64, num_layers=2)
model.eval()
input_data = torch.randn(
    1, 3, 64
)  # Example input data with shape (batch_size, sequence_length, dim)
attn_mask = torch.tril(torch.ones(3, 3))  # Lower triangular attention mask
print("time step 1:")
output = model(input_data, attn_mask=attn_mask)
print("\n\ntime step 2:")
input_data = torch.cat((input_data, torch.randn(1, 1, 64)), 1)
attn_mask = torch.tril(torch.ones(4, 4))  # Lower triangular attention mask
output = model(input_data, attn_mask=attn_mask)
# 输出结果：
# time step 1:
# layer_idx: 0
# q.sum(-1) = [31.20478057861328, 34.04328536987305, 33.6611328125]
# k.sum(-1) = [31.446550369262695, 29.15508460998535, 29.265644073486328]
# v.sum(-1) = [30.789640426635742, 33.80058670043945, 32.4859619140625]
# attention_weights =
#  tensor([[1.0000, 0.0000, 0.0000],
#         [0.6760, 0.3240, 0.0000],
#         [0.2452, 0.4188, 0.3360]], grad_fn=<SqueezeBackward0>)
# ####################################################################################################
# layer_idx: 1
# q.sum(-1) = [30.214162826538086, 34.45262145996094, 26.357181549072266]
# k.sum(-1) = [29.88446617126465, 31.186325073242188, 31.727235794067383]
# v.sum(-1) = [23.99290657043457, 35.66062545776367, 33.28850173950195]
# attention_weights =
#  tensor([[1.0000, 0.0000, 0.0000],
#         [0.3310, 0.6690, 0.0000],
#         [0.4525, 0.3270, 0.2204]], grad_fn=<SqueezeBackward0>)
# ####################################################################################################
# time step 2:
# layer_idx: 0
# q.sum(-1) = [31.20478057861328, 34.04328536987305, 33.6611328125, 27.077472686767578]
# k.sum(-1) = [31.446550369262695, 29.15508460998535, 29.265644073486328, 27.211992263793945]
# v.sum(-1) = [30.789640426635742, 33.80058670043945, 32.4859619140625, 29.695066452026367]
# attention_weights =
#  tensor([[1.0000, 0.0000, 0.0000, 0.0000],
#         [0.6760, 0.3240, 0.0000, 0.0000],
#         [0.2452, 0.4188, 0.3360, 0.0000],
#         [0.1818, 0.2616, 0.2813, 0.2752]], grad_fn=<SqueezeBackward0>)
# ####################################################################################################
# layer_idx: 1
# q.sum(-1) = [30.214162826538086, 34.45262145996094, 26.357181549072266, 29.209003448486328]
# k.sum(-1) = [29.88446617126465, 31.186325073242188, 31.727235794067383, 26.988731384277344]
# v.sum(-1) = [23.99290657043457, 35.66062545776367, 33.28850173950195, 27.92920684814453]
# attention_weights =
#  tensor([[1.0000, 0.0000, 0.0000, 0.0000],
#         [0.3310, 0.6690, 0.0000, 0.0000],
#         [0.4525, 0.3270, 0.2204, 0.0000],
#         [0.2740, 0.0698, 0.4069, 0.2492]], grad_fn=<SqueezeBackward0>)
# ####################################################################################################

可以看到随着时间步的推移，每一层的 x / q / k / v / attention weight 的前 n-1 个 token feature 都和上一个时间步相同，因此可以缓存

Thought

  • 由于在 t 时间步，需要计算 QtQ^t 和 K0,1,...,t, V0,1,...,tK^{0,1,...,t},\ V^{0,1,...,t} 之间的内积，所以需要换成 key / value 的缓存，而不是 query 的缓存
  • paged attention 是通过类似内存分页管理的方式管理 kv cache 的一种方法，动态分配显存，速度更快，支持更高 batch

Posted on Edited on In Valine:

URL

TL;DR

  • FlashAttention-2 是 FlashAttention 一作对前一版的更新，基本思想不变，只优化了部分算法流程，可以比 V1 提速一倍

Algorithm

flash_attention_2.png

  • Flash Attention 2 前向过程主要优化了几个方面：
    1. Flash Attention v1 中计算 P_ij 计算过程很绕，需要更新两次全局信息，v2 中进行了优化
    2. Flash Attention v1 中内外层循环设置不合理，v2 对调了内外层循环，这样做的好处是：
    3. 不再需要重复读入写出 O
    4. max_value 信息变成一个计算中间变量，不再需要读入写出，backward 过程也无需依赖
  • Flash Attention v2 和 Flash Attention v1 的 IO 量对比
    • v1：
      • 读：2Nd+2TcNd2Nd+2T_cNd
      • 写：TcNd+2TcNT_cNd+2T_cN
    • v2：
      • 读：Nd+2TrNdNd+2T_rNd
      • 写：Nd+NNd+N
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import torch
import math
BLOCK_SIZE = 1024
NEG_INF = -1e10  # -infinity
EPSILON = 1e-10
def flash_attention2_forward(Q, K, V):
    batch, seq_len, dim = Q.shape
    O = torch.zeros_like(Q, requires_grad=True, device=Q.device)
    l = torch.zeros((batch, seq_len, 1), device=Q.device)  # 1 for broadcasting
    m = torch.ones((batch, seq_len, 1), device=Q.device) * NEG_INF
    Q = list(torch.split(Q, BLOCK_SIZE, dim=1))
    K = list(torch.split(K, BLOCK_SIZE, dim=1))
    V = list(torch.split(V, BLOCK_SIZE, dim=1))
    O = list(torch.split(O, BLOCK_SIZE, dim=1))
    l = list(torch.split(l, BLOCK_SIZE, dim=1))
    m = list(torch.split(m, BLOCK_SIZE, dim=1))
    Tr = len(Q)
    Tc = len(K)
    scale = 1 / math.sqrt(dim)
    for i in range(Tr):
        Qi_scaled = Q[i] * scale
        for j in range(Tc):
            S_ij = torch.einsum("bnd,bmd->bnm", Qi_scaled, K[j])
            m_ij, _ = torch.max(S_ij, dim=-1, keepdim=True)
            mi_new = torch.maximum(m_ij, m[i])
            P_ij = torch.exp(S_ij - mi_new)
            P_ijV_j = torch.einsum("bnm,bmd->bnd", P_ij, V[j])
            exp_row_max_diff = torch.exp(m[i] - mi_new)
            li_new = l[i] * exp_row_max_diff + P_ij.sum(dim=-1, keepdim=True)
            O[i] = O[i] * exp_row_max_diff + P_ijV_j
            m[i] = mi_new
            l[i] = li_new
        O[i] = O[i] / l[i]
    O = torch.cat(O, dim=1)
    l = torch.cat(l, dim=1)
    return O, l
def flash_attention2_backward(Q, K, V, O, l, dO):
    # 参考代码中进行了实现，但这里省略，重点关注一下 backward 过程的输入
    pass
if __name__ == "__main__":
    device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
    # batch, seq_len, dim
    Q = torch.randn(2, 4096, 128, requires_grad=True).to(device)
    K = torch.randn(2, 4096, 128, requires_grad=True).to(device)
    V = torch.randn(2, 4096, 128, requires_grad=True).to(device)
    flash2_out = flash_attention2_forward(Q, K, V)
    print(flash2_out[0].sum().item())
  • backward 过程在 v2 论文中详细的写出来了，如下：
    flash2_2.png
  • 速度效果提升很明显
    flash2_3.png

Thought

  • Flash Attention v2 看起来特别像 Flash Attention 的紧急修复版本，把之前写的冗余删掉了
  • 甚至完全不了解 Flash Attention 思想的人看 Flash Attention 的实现代码，都可以将其优化到 Flash Attention v2，就是简单的代码优化…
  • Flash Attention v2 彻底把这个 tiling 思路的优势发挥出来了