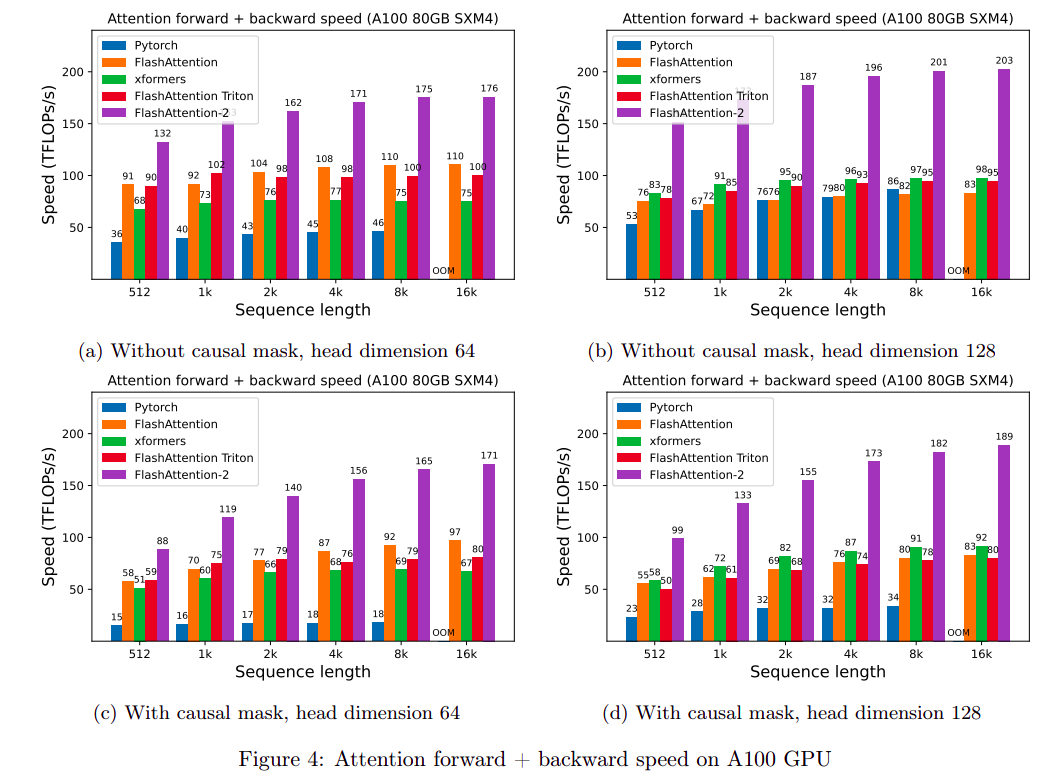
URL
- paper: https://arxiv.org/pdf/2108.12409
- code: https://github.com/ofirpress/attention_with_linear_biases/blob/a35aaca144e0eb6b789dfcb46784c4b8e31b7983/fairseq/models/transformer.py#L742
TL;DR
- 本文提出一种比
T5 bias更简单的position embedding方法叫做ALiBi (Attention with Linear Bias),简单好用 - 可以在短数据集上训练,在长数据集上测试,即具有外推性
Algorithm
T5 bias
- 先讲一下
T5 bias是如何实现position embedding的,主要分三步:- 计算
query / key的n * n相对位置矩阵,形如:1
2
3
4
5
6
7
8
9
10[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[-1, 0, 1, 2, 3, 4, 5, 6, 7, 8],
[-2, -1, 0, 1, 2, 3, 4, 5, 6, 7],
[-3, -2, -1, 0, 1, 2, 3, 4, 5, 6],
[-4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4],
[-6, -5, -4, -3, -2, -1, 0, 1, 2, 3],
[-7, -6, -5, -4, -3, -2, -1, 0, 1, 2],
[-8, -7, -6, -5, -4, -3, -2, -1, 0, 1],
[-9, -8, -7, -6, -5, -4, -3, -2, -1, 0]] - 将相对位置矩阵分桶(超过
num_buckets的饱和到num_buckets)1
2
3
4
5
6
7
8
9
10[[ 0, 17, 18, 19, 20, 21, 22, 23, 24, 24],
[ 1, 0, 17, 18, 19, 20, 21, 22, 23, 24],
[ 2, 1, 0, 17, 18, 19, 20, 21, 22, 23],
[ 3, 2, 1, 0, 17, 18, 19, 20, 21, 22],
[ 4, 3, 2, 1, 0, 17, 18, 19, 20, 21],
[ 5, 4, 3, 2, 1, 0, 17, 18, 19, 20],
[ 6, 5, 4, 3, 2, 1, 0, 17, 18, 19],
[ 7, 6, 5, 4, 3, 2, 1, 0, 17, 18],
[ 8, 7, 6, 5, 4, 3, 2, 1, 0, 17],
[ 8, 8, 7, 6, 5, 4, 3, 2, 1, 0]]这里上三角和下三角都有值是因为
encoder bidirection=True,如果是decoder,则如下:1
2
3
4
5
6
7
8
9
10[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[2, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[3, 2, 1, 0, 0, 0, 0, 0, 0, 0],
[4, 3, 2, 1, 0, 0, 0, 0, 0, 0],
[5, 4, 3, 2, 1, 0, 0, 0, 0, 0],
[6, 5, 4, 3, 2, 1, 0, 0, 0, 0],
[7, 6, 5, 4, 3, 2, 1, 0, 0, 0],
[8, 7, 6, 5, 4, 3, 2, 1, 0, 0],
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]] - 最后是将此
n * n的relative position bucket通过可学习的embedding函数变成n * n * num_heads的向量,和每个头的attention score(softmax 之前)相加,然后通过逐行softmax得到attention weight
- 计算
ALiBi

- 用数学公式表示:
ALiBi的计算和T5 bias的前两步几乎一模一样- 第三步不再使用可学习的
embedding函数映射到每个头上,而是将距离矩阵的值和每个头独立的 不可学习的 常量m值相乘,然后和attention score相加 -
b是一个基数H是注意力头的数量h是注意力头的索引(从0到H-1)
Thought
- 标准
attention的 已经慢慢被淘汰了,不管是RoPE / T5 Bias / ALiBi都已经逐渐演变成 直接作用在attention score上了 ALiBi的外推性其实本质是强行饱和掉远距离,有点过于粗暴了…