Zhangzhe's Blog

The projection of my life.

0%

Posted on Edited on In Valine:

TL;DR

  • 《俄罗斯方块》这部电影里游戏作者用命令行玩俄罗斯方块原型机太酷了，所以决定自己实现一把
    tetris.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
import numpy as np
from func_timeout import FunctionTimedOut, func_set_timeout
from copy import deepcopy
import keyboard
from random import choice
def random_choice_block():
    blocks = [
        (
            # .  .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  .  . [x][x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
            ),
        ),
        (
            # .  .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  .  .  . [x][x] .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 2],
                [0, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
            ),
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2 - 1],
            ),
        ),
        (
            # .  .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  . [x][x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [0, space.shape[1] // 2 + 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
            ),
            # .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2],
            ),
        ),
        (
            # .  .  .  .  .  . [x][x][x][x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 2],
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [0, space.shape[1] // 2 + 1],
            ),
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2],
                [3, space.shape[1] // 2],
            ),
        ),
        (
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [1, space.shape[1] // 2 + 1],
            ),
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  .  . [x][x] .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2 - 1],
            ),
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [0, space.shape[1] // 2 + 1],
                [1, space.shape[1] // 2],
            ),
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            # .  .  .  .  . [x][x] .  .  .  .  .
            # .  .  .  .  .  . [x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2],
            ),
        ),
        (
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [1, space.shape[1] // 2 + 1],
            ),
            # .  .  .  .  . [x][x] .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2 - 1],
                [2, space.shape[1] // 2 - 1],
            ),
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            # .  .  .  .  .  .  . [x] .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [0, space.shape[1] // 2 + 1],
                [1, space.shape[1] // 2 + 1],
            ),
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  . [x][x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2 - 1],
                [2, space.shape[1] // 2],
            ),
        ),
        (
            # .  .  .  .  .  .  . [x] .  .  .  .  .
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            (
                [0, space.shape[1] // 2 + 1],
                [1, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2],
                [1, space.shape[1] // 2 + 1],
            ),
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x][x] .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [1, space.shape[1] // 2 - 1],
                [2, space.shape[1] // 2 - 1],
                [2, space.shape[1] // 2],
            ),
            # .  .  .  .  . [x][x][x] .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [0, space.shape[1] // 2 + 1],
                [1, space.shape[1] // 2 - 1],
            ),
            # .  .  .  . [x][x] .  .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            # .  .  .  .  . [x] .  .  .  .  .  .  .
            (
                [0, space.shape[1] // 2 - 1],
                [0, space.shape[1] // 2],
                [1, space.shape[1] // 2],
                [2, space.shape[1] // 2],
            ),
        ),
    ]
    return choice(blocks)
def can_transform():
    global block_idx, position
    block = block_list[block_idx]
    next_block = block_list[(block_idx + 1) % len(block_list)]
    shift = (position[1][0] - block[1][0], position[1][1] - block[1][1])
    next_position = np.zeros_like(position, dtype=np.int64)
    for i, p in enumerate(next_block):
        next_position[i][0] = p[0] + shift[0]
        next_position[i][1] = p[1] + shift[1]
    if next_position[:, 0].min() < 0:
        next_position[:, 0] -= next_position[:, 0].min()
    if next_position[:, 0].max() >= space.shape[0]:
        next_position[:, 0] -= next_position[:, 0].max() - space.shape[0] + 1
    if next_position[:, 1].min() < 0:
        next_position[:, 1] -= next_position[:, 1].min()
    if next_position[:, 1].max() >= space.shape[1]:
        next_position[:, 1] -= next_position[:, 1].max() - space.shape[1] + 1
    for p in next_position:
        if space[p[0], p[1]] and list(p) not in position.tolist():
            return False
    for p in position:
        space[p[0], p[1]] = False
    position = next_position
    block_idx = (block_idx + 1) % len(block_list)
    return True
def transform():
    if can_transform():
        for p in position:
            space[p[0], p[1]] = True
    show_space()
def get_block():
    global position
    global block_list
    global block_idx
    global next_block_list
    global next_block_idx
    if position is not None:
        block_list = next_block_list
        block_idx = next_block_idx
    else:
        block_list = random_choice_block()
        block_idx = choice([i for i in range(len(block_list))])
    block = block_list[block_idx]
    next_block_list = random_choice_block()
    next_block_idx = choice([i for i in range(len(next_block_list))])
    for p in block:
        if space[p[0], p[1]]:
            show_space()
            return False
    for p in block:
        position = np.array(
            block,
            dtype=np.int64,
        )
        space[p[0], p[1]] = True
    show_space()
    return True
def can_down():
    down_position = deepcopy(position)
    down_position[:, 0] += 1
    if down_position[:, 0].max() >= space.shape[0]:
        return False
    for dp in down_position:
        if dp.tolist() not in position.tolist() and space[dp[0], dp[1]]:
            return False
    return True
def can_cancel_layer():
    for i, line in enumerate(reversed(space)):
        if line.sum() == len(line):
            return len(space) - i - 1
    return -1
def cancel_layer(layer_label):
    global score
    space[1 : layer_label + 1] = space[:layer_label]
    space[0, :] = False
    score += 100
def down():
    if can_down():
        for p in position:
            space[p[0], p[1]] = False
        position[:, 0] += 1
        for p in position:
            space[p[0], p[1]] = True
    show_space()
def can_left():
    left_position = deepcopy(position)
    left_position[:, 1] -= 1
    if left_position[:, 1].min() < 0:
        return False
    for lp in left_position:
        if lp.tolist() not in position.tolist() and space[lp[0], lp[1]]:
            return False
    return True
def left():
    if can_left():
        for p in position:
            space[p[0], p[1]] = False
        position[:, 1] -= 1
        for p in position:
            space[p[0], p[1]] = True
    show_space()
def can_right():
    right_position = deepcopy(position)
    right_position[:, 1] += 1
    if right_position[:, 1].max() >= space.shape[1]:
        return False
    for rp in right_position:
        if rp.tolist() not in position.tolist() and space[rp[0], rp[1]]:
            return False
    return True
def right():
    if can_right():
        for p in position:
            space[p[0], p[1]] = False
        position[:, 1] += 1
        for p in position:
            space[p[0], p[1]] = True
    show_space()
def show_space():
    print()
    print("=" * 10 + "\tNEXT\t" + "=" * 10)
    block = np.array(next_block_list[next_block_idx])
    block[:, 1] -= block[:, 1].min()
    next_block = np.zeros((4, 4), dtype=np.bool8)
    for p in block:
        next_block[p[0], p[1]] = True
    for line in next_block:
        s = ""
        for item in line:
            if item:
                s += "[X]"
            else:
                s += " . "
        print(s)
    print()
    print("=" * 10 + "\tGAME AREA\t" + "=" * 10)
    for line in space:
        s = ""
        for item in line:
            if item:
                s += "[X]"
            else:
                s += " . "
        print(s)
    print("-" * 30 + f"\tSCORE: {score}\t" + "-" * 30)
def keyboard_callback(event: keyboard.KeyboardEvent):
    if event.event_type == "down":
        if event.name == "left":
            left()
        elif event.name == "right":
            right()
        elif event.name == "down":
            down()
        elif event.name == "up":
            transform()
@func_set_timeout(1)
def listen_keyboard():
    keyboard.hook(callback=keyboard_callback, suppress=True)
    keyboard.wait()
def main():
    while get_block():
        while can_down():
            try:
                listen_keyboard()
            except FunctionTimedOut:
                down()
        try:
            listen_keyboard()
        except FunctionTimedOut:
            while can_cancel_layer() > -1:
                cancel_layer(can_cancel_layer())
    print(f"score: {score}\tgame over !!!")
if __name__ == "__main__":
    space_shape = (20, 10)
    score = 0
    space = np.zeros(shape=space_shape, dtype=np.bool8)
    position = None
    main()

遇到的问题

  • python 监听字符读入（非 input，input 需要回车结束）好困难，所以该程序 必须用 root 用户下命令行运行…
  • python 的超时阻塞式监听更难，func_timeout 在 linux 上运行疑似还有 bug：多线程打开文件但没有关闭，超出 OS limit，在玩十分钟可能才会出现…

Posted on Edited on In Valine:

Topic

  • 本文汇总多种 语义分割算法 decode head 结构和 部分分割专用 backbone，用于理解语义分割算法的演进过程
  • decode head 模型来源： mmsegmentaion decode head
  • 本文的语义分割 decode head 是指满足如下要求的网络结构：
    1. 输入为 backbone / neck 提取的 feature map 或 feature map list
    2. 输出为 segmentation 结果

语义分割推理过程

1. 原始特征处理

  • 输入的原始特征包括两类：
    • backbone 输出的 feature map（例如 PSPNet 输出）
    • backbone 不同阶段 / neck (例如 FPN) 输出的不同尺度的 feature map list
  • 对于 feature map，可以 resize 到输出大小再送入 decode head，也可以直接送入 decode head，根据具体算法选择
  • 对于 feature map list，一般有两种做法，根据具体算法选择：
    1. resize concat: 将所有 feature map 全部 resize 到输出大小后再 concat（例如 FCN-8s）
    2. multiple select: 根据 index 在 feature map list 中索引并输出对应的 feature map sub list

2. 特征解码

  • 将 1 中输出的 feature map / feature map list 转化成与输出 宽高一致 的 feature map，也是本文具体展开讲的内容

3. 特征映射到分割任务空间

  • 将 2 中输出的特征映射到分割空间，具体通道数与任务定义相关（例如：二分类的语义分割输出通道为 1 或 2，N 分类的语义分割输出通道数为 N）

演进过程

第一代：在 CNN 结构上创新

  • FCN: 2014年，出自 UC Berkeley，分割算法起点
  • PSP: 2016年，出自商汤，FCN + 多尺度
  • ASPP: 2017年，出自 Google，PSP 的优雅实现版（DeepLab V2、DeepLab V3）
  • FPN: 2018年，出自 FAIR，UNet 多尺度的升级版
  • UperNet: 2018年，出自旷视，PSP + FPN 更暴力的多尺度
  • DepthwiseSeparableASPP: 2018年，出自 Google，DeepLab V3 结构的小改动（DeepLab V3+）
  • DepthwiseSeparableFCN: 2019年，出自东芝 + 剑桥，FCN 的轻量化改造（Fast-SCNN）
  • PointRend: 2019年，出自 FAIR，在其他 decode head 基础上级联了一个 subnetwork 实现了图像分割边缘的细化

第二代：Self-Attention (Non-local / Channel Attention)

  • Non-Local: 2017年，出自 FAIR，Self Attention 经典
  • PSANet: 2018年，出自商汤，Non-local 的二维 狗尾续貂 版
  • CCNet: 2018年，出自地平线，Non-local 的低算力版，使用两个低算力的 Attention 替代 Non-local Attention
  • DANet: 2018年，出自京东，两路 Non-local，一路 attention to postion 一路 attention to channel
  • EncNet: 2018年，出自商汤 + Amazon，优化了 SENet 中的暴力编码方式，在分割任务中额外加入了分类辅助监督
  • EMANet: 2019年，出自北大，attention to channel 和 attention to postion 可分离的 attention
  • ANN: 2019年，出自华中科技大学，简化 Non-local 同时引入 PPM，极大的降低了 matmul 和 softmax 两类算子的耗时
  • GCNet: 2019年，出自 MSRA，简化版 Non-local + SENet 的缝合怪
  • OCRNet: 2019年，出自 MSRA，级联结构，在其他 decode head 的输出结果上做了 Self-Attention，并在论文中从 Transformer 角度解释了 Self-Attention（Transformer 开始觉醒）
  • APCNet: 2019年，出自商汤，复杂网络结构 + 简化矩阵乘实现的 Attention
  • DMNet: 2019年，出自商汤，根据输入特征的全局信息动态生成卷积核，本质也是 Attention
  • LRASPP: 2019年，出自 Google，全局 scale 实现的 Attention（MobileNet V3）
  • ISANet: 2019年，出自 MSAR，使用 feature map shuffle 实现长范围和短范围的稀疏注意力机制
  • DNLNet: 2020年，出自 MSAR，改进 Non-local，加入了归一化和一元分支
  • BiSeNet: 2019年，出自旷视，在 backbone 之外加入了一个 context branch，将特征提取和 attention 解耦，降低了 attention 恐怖的计算量
  • BiSeNet V2: 2020年，出自腾讯，BiSeNet 的改进
  • SDTC: 2021年，出自美团，BiSeNet 系列的改进版，但由于融合了两路分支到一处，不再 Bilateral，所以用特征提取 SDTC block 命名…

第三代：Transformer

  • SETR: 2020年，出自腾讯，Vit 做 backbone + FCN / FPN decode head
  • DPT: 2021年，出自 Intel，SETR 的升级版，backbone 不变，decode head 更 FPN 了一些
  • Segmenter: 2021年，出自法国 INRIA 研究所，用了纯 Transformer 架构而不是像 SETR / DPT 一样用 Transformer Encoder + CNN Decoder 架构
  • SegFormer: 2021年，出自 NVIDIA，SETR 的高效版
  • KNet: 2021年，出自商汤，decode head 融合了 Channel Attention + Multi-head Attention + RNN，统一了语义分割、实例分割、全景分割框架

Algorithms

1. FCN

1.1 原始特征处理

  • 原始特征处理使用了 resize concat 方式，将多个不同尺度（backbone 不同阶段）的 feature map resize concat 到输出尺寸，如下图所示：
    FCN1.png
    FCN2.png

实验证明越多尺度融合分割效果越好

1.2 特征解码

  • 特征解码只使用了几层普通 Conv + 可选择的 concat input （shortcut）结构

2. PSP

2.1 原始特征处理

  • PSPNet 的原始特征是 backbone 最后一层的输出，所以无需原始特征处理

2.2 特征解码

  • PSPNet 将输入特征通过 Pyramid Pooling Module 结构做了 feature map 不同尺度 down sample + up sample，如下图所示：
    PSP.png

3. ASPP

3.1 原始特征处理

  • DeepLabV3 输入为单个单尺度 feature map，所以此步骤可省略

3.2 特征解码

ASPP.png

与 PSPNet 很像，PSPNet 是使用普通 Conv 去卷积多种尺度的 Pooled feature map；ASPP 是不改变 feature map 而是使用 不同空洞系数的 Conv

4. FPN

5. UperNet

5.1 原始特征处理

  • 本算法在 decode head 中内嵌使用 FPN（而不是以网络 neck 方式使用），所以 feature map list 格式的原始特征无需处理，直接透传到特征解码部分

5.2 特征解码

UperNet.png

本文只讨论图中蓝色框部分
UperNet_2.png
只需要看蓝色框为输出的通路，算法：

  1. 在最小尺度 feature map 上使用 PPM（全称 Pyramid Pooling Module，来自于 PSPNet）
  2. 使用 FPN 融合多尺度特征

6. DepthwiseSeparableASPP

相较于 DeepLab V3 在 8 倍下采样的 feature map 上使用 ASPP，DeepLab V3+ 在更小尺度(16 倍下采样) feature map 上使用 DepthwiseSeparable ASPP
同时为了解决小尺度预测的问题，加入了一个 vanilla FPN 做不同尺度特征融合

7. DepthwiseSeparableFCN

图中的 DWConv 是指 Depthwise Conv（ic == oc == group）
图中的 DSConv 是指 Depthwise Separable Conv，DSConv 不是一个 Conv 而是 Depthwise Conv 和 Pointwise Conv（kernel_size == 1 and group == 1） 以及激活函数 / BN 一起组成的一个 block

8. PointRend

  • 渲染：渲染（render）是指在电脑中使用三维制作软件将制作的模型经过纹理、绑定、动画、灯光处理后得到模型和动画的图像。三维渲染是使用计算机从数字三维场景中生成二维影像的过程
  • 细分表面算法：细分表面算法（subdivision surface algorithm）在3D计算机图形中使用，通过递归完善基本级多边形网格来创建弯曲表面
    point2.png
  • 本文的核心思想：
    • 将计算机图形学中的 Subdivision render 思想用于分割，使用 coarse-to-fine 思想，逐级细分，提高分割效果
    • 使用非均匀采样方法，越高频的区域使用越多的采样点，提高边缘分割效果
      point3.png
      point4.png
  • Inference 过程（以 FCN 作为 prev_decode_head 为例）:
    • 输入：
      • backbone 的输出 x，shape = [batch, channels, height, width]
      • FCN 的输出 prev_output，shape = [batch, num_cls, height, width]
    • 输出：refine 后的输出，shape = [batch, num_cls, 2 * subdivision_steps * height, 2 * subdivision_steps * width]
    1. prev_output copy 一份作为 refined_seg_logits
    2. refined_seg_logits 插值放大两倍，shape = [batch, num_cls, 2 * height, 2 * width]
    3. 在 refined_seg_logits 上挑选最 hard 的 N 个点（hard 的定义是：如果一个像素的 top1_cls_logitis 和 top2_cls_logits 越接近，则该点越 hard），输出相对坐标，shape = [batch, N, 2]
    4. 根据选出的 N 个点的坐标在 x 中找到对应的点（需要插值找出），作为 fine_grained_point_feats，shape = [batch, channels, N]
    5. 根据选出的 N 个点的坐标在 prev_output 中找到对应的点（需要插值找出），作为 coarse_point_feats，shape = [batch, num_cls, N]
    6. fine_grained_point_feats 和 coarse_point_feats concat 后经过 Subnetwork（几层 MLP）映射到类别空间 point_logits，shape = [batch, num_cls, N]
    7. 根据 3 中的 point index，将 6 输出的 point_logits 替换到 1 中的 refined_seg_logits 对应位置
    8. 重复 2 ~ 7 subdivision_steps 次，输出最终的 refined_seg_logits，shape = [batch, num_cls, 2 * subdivision_steps * height, 2 * subdivision_steps * width]
  • Train 过程：
    • 输入：
      • backbone 的输出 x，shape = [batch, channels, height, width]
      • FCN 的输出 prev_output，shape = [batch, num_cls, height, width]
      • gt_semantic_seg，shape = [batch, num_cls, height, width]
    • 输出：loss
    • Train 过程与 Inference 过程基本相同，区别在于：
      • 由于 topk 运算对梯度反向传播不友好，所以在 Train 的过程中使用随机采样点的策略，没有挖掘 hard case
      • Train 不会引入多尺度，只会在同一尺度学习 subnetwork 对 point 的分类

9. Non-Local

用于 2 维图像，所以 T == 1，通过增加 (HW, HW) 的特征相关性矩阵给特征带来全局相关性（Attention）

  • decode head 前后处理和 FCN 一致

10. PSANet

借鉴于 Non-local，强行给了比较牵强的数学解释，推理过程复杂到需要调用 CUDA 而不是使用 pure pytorch

11. CCNet

使用两个十字交叉注意力模块的串联替代 Non-local，降低算力
CC2.png
整体流程平平无奇

  • decode head 前后处理和 FCN 一致

12. DANet

13. EncNet

对于 SE-loss: 监督图中包含哪些类别的像素，使用交叉熵实现
对于 Encode:

  • 从本质上看：
    • 上图使用的 Encode 和 SENet (Squeeze and Excitation Network) 对 feature map per channel 编码没有区别
  • 从实现层面看：
    1. Encode 使用了更在数学上更好解释的编码方式（而不是 SENet 粗暴的 Global Average Pooling 编码方式）
    2. Encode 编码空间比 SENet 更大（SENet 每个通道使用 R\mathbb{R} 空间编码，Encode 每个通道使用 Rd\mathbb{R}^d 空间编码）

14. EMANet

15. ANN

在 key / value 上对特征进行了降维 N -> S，由下图可知，上图的 sample 方法具体是指 PPM（Pyramid Pooling Module）
ANN2.png
AFNB 全称是 Asymmetric Fusion Non-local Block
APNB 全称是 Asymmetric Pyramid Non-local Block
二者对 Non-local 的 Self-Attention 进行简化，例如 share key value

16. GCNet

Non-local 结构的化简
GC.png
作者认为一个全局上下文建模结构如图 (a) 所示
图 (b) 为简化后的 Non-local 结构
图 © 是 SENet 结构
图 (d) 是本文提出的 GC 结构

  • decode head 前后处理和 FCN 一致

17. OCRNet

上图中粉红色的部分即为 OCRNet decode head
OCR2.png
论文中给出的算法架构图，给中间结果赋予了可解释的含义

18. APCNet

19. DMNet

之前的网络结构都是通过空洞卷积或大卷积核实现多尺度
DMNet 通过输入特征的 Adaptive Pooling 生成动态卷积核实现多尺度
DMNet.png

20. LRASPP

21. ISANet

  • 利用 feature map 重排实现长范围或短范围的稀疏注意力。

22. DNLNet

DNL 结构（图 d）在原始 Non-local 结构（图 a）上做了如下改动：

  1. 加入了一元 Non-local 分支 Unary Non-local
  2. 在二元分支矩阵乘之前加入了白化操作（ H*W 维度减均值，相当于 instance norm）
    DNL2.png
    由于减了均值，所以二元分支上 “+” 这一点在 Attention map ∈RHW×HW\in \mathbb{R}^{HW\times HW} 上的索引 heat map ∈RH×W\in \mathbb{R}^{H\times W} 变干净很多（相当只学习残差）
    这张图也从侧面反映了 Non-local 还是很强的，Attention 不是在讲故事

23. BiSeNet

  • backbone 主要分成两个分支 spatial path 和 context path，本质就是在基础 backbone 的基础上加入了一个计算量（通道数）非常小的 attention branch 增加上下文信息，最后融合两通道特征送入 decode head
  • decode head 就是基础的 FCN

24. BiSeNet V2

对 BiSeNet 主要改进有:

  • context branch 上增加了更多更复杂的模块，可更好收集上下文信息
  • context branch 上增加了更多监督，每个尺度上都有监督损失
  • 分支融合模块设计的更加复杂

25. SDTC

很新颖的 Loss 设计，效果和计算量都优于 BiSeNet 系列
SDTC2.png
这就是 SDTC 模块

26. SETR

  • 本质是 Vit（vision transformer） 做 backbone，FCN / 类似 FPN 做 decode head 的分割算法
  • 为了缩减计算量，Vit 会将原图剪成多个 patch（worth 16x16 words...），每个 patch 单独输入到 24 层 Transformer Encoder 中，每个 patch 内部独立做全局 attention
  • 剪 patch 带来的问题是：与其他 CNN backbone + decode head 结构不同，Transformer backbone + decode head 结构中 decode head 需要顺序 inference 每个 patch feature（注意图a Decoder 输入为多个 patch feature），最后拼回到整张图大小
  • SETR_UPU decode head == sequence FCN
  • SETR_MLA decode head == sequence FPN（Attention 不改变输入宽高，所以不存在严格意义上的 多尺度，只是不同网络深度的特征）

27. DPTNet

  • 本质和 SETR 一样都是使用 Vit 做 backbone
  • 和 SETR 不同的地方在于：
    • 不同 backbone 深度特征融合方式更复杂，更接近 FPN
    • decode head 不再是输入 sequence patch feature，而是输入融合后的全图 feature

28. Segmenter

  • 用了纯 Transformer 架构（Transformer Encoder + Decoder），SETR 和 DPT 都是 Transformer Encoder + CNN Decoder

29. SegFormer

  • backbone 不再是标准 Transformer Encoder（Vit），而是改成了更轻量化的 MixVisionTransformer（Mit）
    • Mit 使用了更大的 patch 且 patch 之间存在 overlap
    • Mit 使用了 coarse-to-fine 的特征表示，随着 Transformer Encoder 变深 feature map 宽高变小
    • Mit 使用了更简单的 Self-Attention 公式
    • Mit 去掉了 position embeding，使用了 Mix-FFN
  • decode head 使用了纯 MLP，且很自然的融合了多尺度（真.多尺度）

30. KNet

从框架上统一了三种分割方式
KNet.png
红字标出的是每个张量的 shape
绿字标出的是每个计算过程实际是在做什么
上述过程会像 RNN 一样循环多次去更新 kernel，使得结果更好（重复使用 backbone 的输出）

Posted on Edited on In Valine:

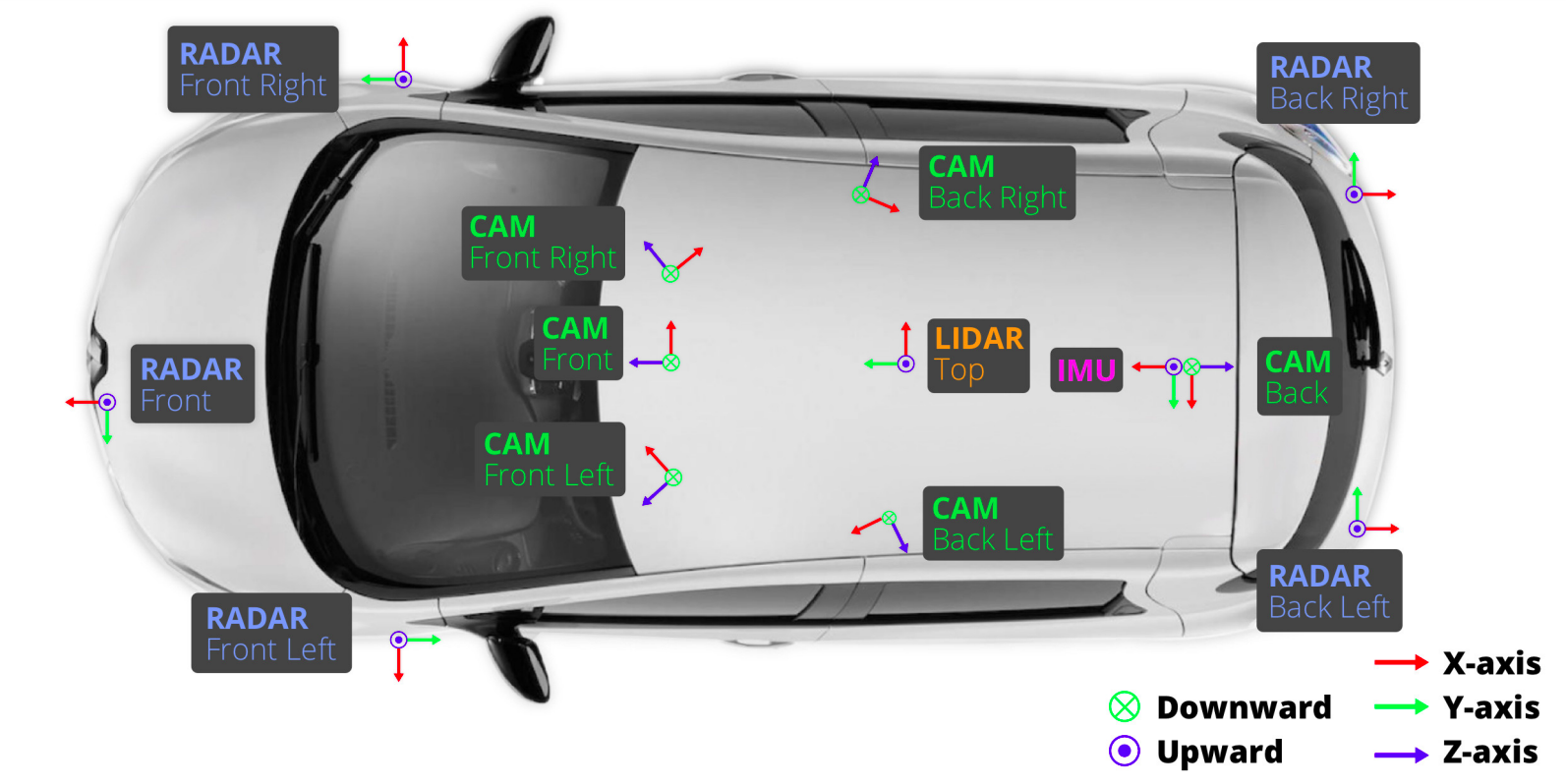
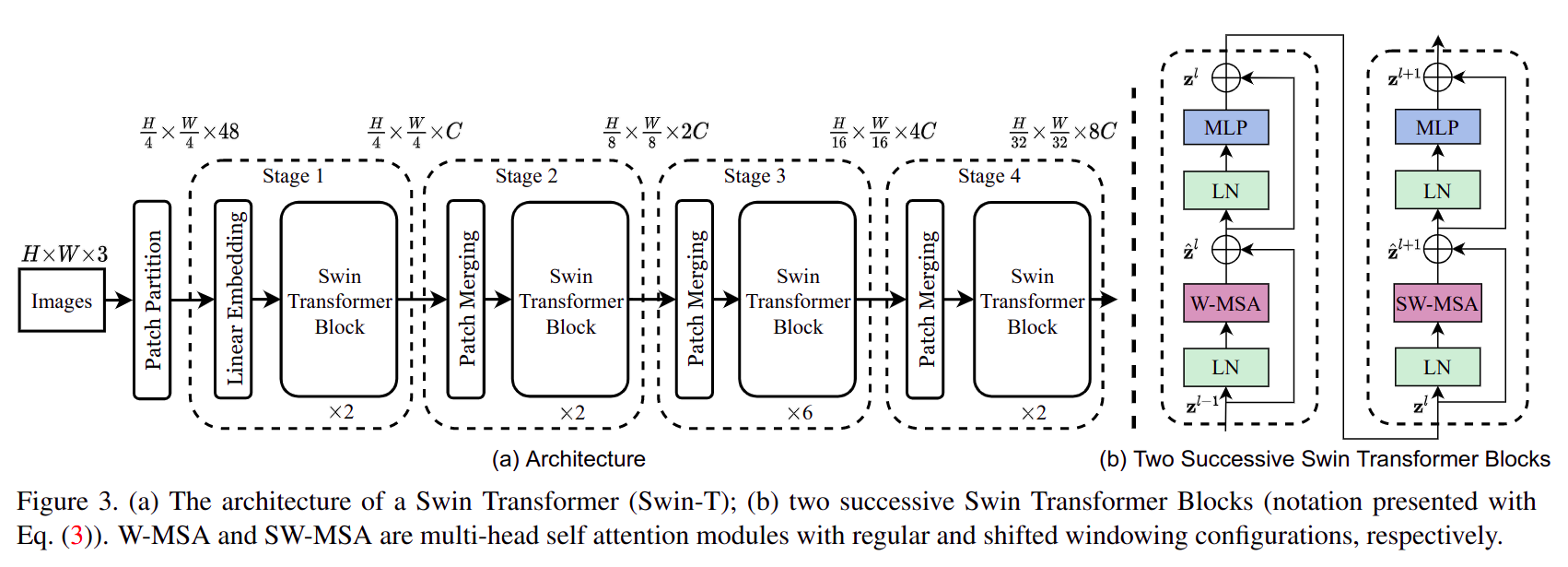
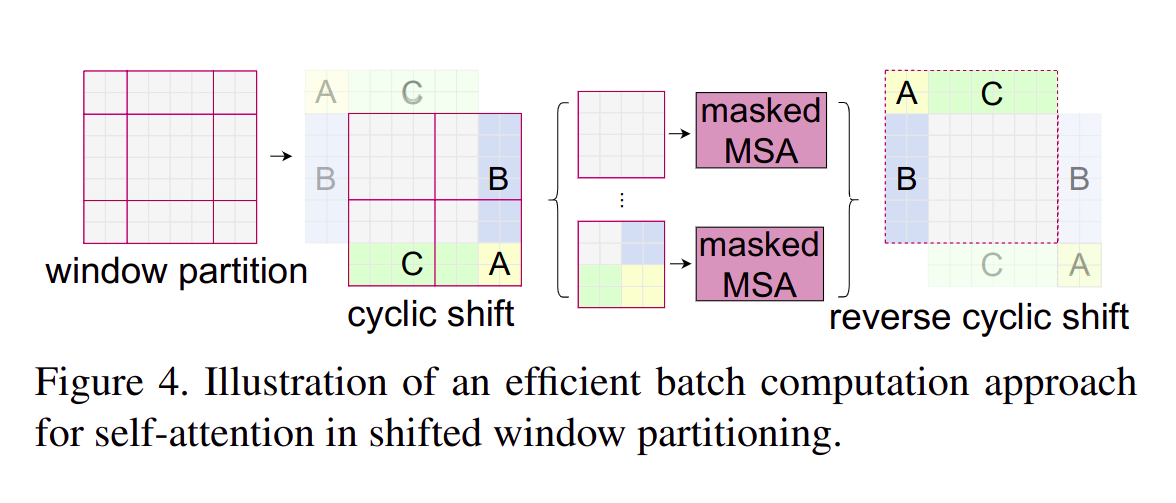
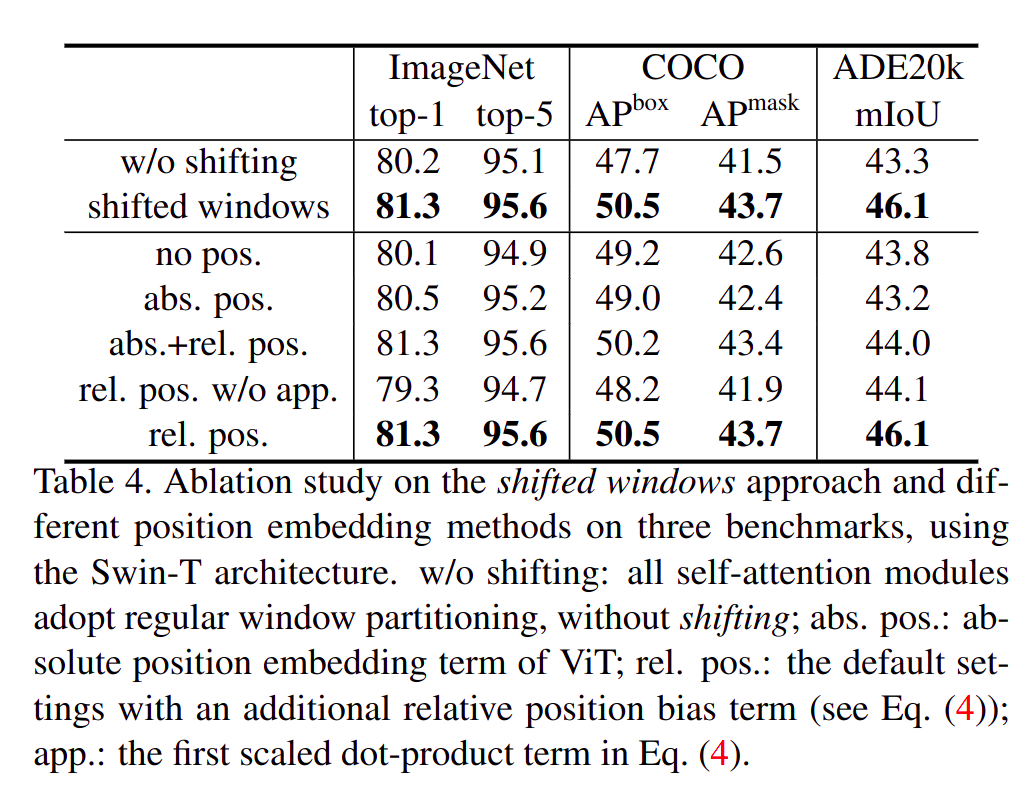
URL

Algorithm

TL;DR

  • 本文提出一种 最大编码率降低（MCR2） 表征算法，本质是一种表征损失函数，本算法有效优化了表征空间，在有监督学习（分类）与自监督学习（聚类）都取得了不错的效果。

Maximal Coding Rate Reduction

  • 什么是一个好的表征？一个好的表征应该有哪些性质？
    • 一个好的表征应该充分利用表征空间。
    • 一个好的表征在同一类下的表征应该尽可能的相似。
  • MCR2MCR^2 Loss
    • R(Z,ϵ)=12logdet(I+dmϵ2ZZT)R(Z, \epsilon)=\frac{1}{2}logdet(I+\frac{d}{m\epsilon^2}ZZ^T)
    • Rc(Z,ϵ∣Π)=∑j=1ktr(Πj)2mlogdet(I+dtr(Πj)ϵ2ZΠjZT)R^c(Z,\epsilon|\Pi)=\sum_{j=1}^k\frac{tr(\Pi_j)}{2m}logdet(I+\frac{d}{tr(\Pi_j)\epsilon^2}Z\Pi_j Z^T)
    • max⁡θ∣ΠΔR(Z(θ),Π,ϵ)=R(Z,ϵ)−Rc(Z,ϵ∣Π)\max_{\theta|\Pi} \Delta R(Z(\theta),\Pi,\epsilon)=R(Z, \epsilon)-R^c(Z,\epsilon|\Pi)
    • 其中：

      • Z∈Rd×mZ\in\mathbb R^{d\times m} ，其中 dd 是表征向量的长度，mm 是一个 batch 的大小，典型值是 d=128, m=1000d=128,\ m=1000 。

      • detdet 表示行列式的值， logdetlogdet 表示行列式的值的自然对数。

      • Πj\Pi_j 表示选择函数，选择属于类 jj 的特征向量进行计算。

  • MCR2MCR^2 Loss 解析
    • detdet 行列式函数可以用于衡量一个矩阵中向量的正交程度，行列式的值越大，矩阵中向量越正交，向量实际利用的表征空间越大。
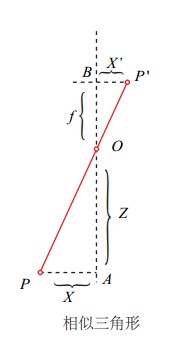
    • A=[abcd]A=\begin{bmatrix} a & b \\ c & d \end{bmatrix} 矩阵的行列式表示由向量 v1=[a,b], v2=[c,d]v_1 = [a, b],\ v_2=[c, d] 组成的平行四边形的面积，如下图所示，当 v1, v2v_1,\ v_2 向量正交时，面积最大，行列式值最大。
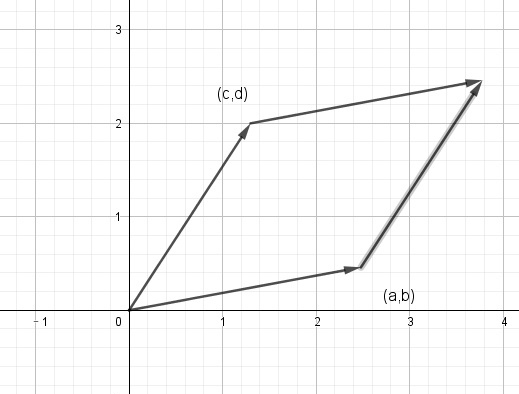
      det.png
    • 同理，在 dd 维空间下，当 dd 个 dd 维空间越正交，组成的 空间积 越大。
    • ZZTZZ^T 是个实对称矩阵，因此是半正定矩阵，因此 I+ZZTI + ZZ^T 是个正定矩阵，因此 I+ZZTI+ZZ^T 的行列式的值 > 0，因此 logdet 有定义。
    • MCR2MCR^2 Loss 的实际含义是：所有表征向量尽可能正交，属于同一个类的表征向量尽可能不正交，因此属于同一个类别的表征向量会尽可能共线，不同类别会尽可能正交。
    • Loss 中的 d, md,\ m 都是平衡因子，平衡因向量的长度和统计集大小引起的数值变化。
  • 在使用 Cifar10 数据集训练后，将输出的 128 维度表征使用任意分类器（SVM / KNN / 单层神经网络）都很容易进行分类，达到 95+ 的准确率。
  • 而且 MCR2MCR^2 Loss 在分类任务中的一个优势在于：对于存在错误标签的数据，MCR2MCR^2 比交叉熵对错误标签的敏感度更低，如下图所示：
    MCR2 and CE.png
  • 面对聚类任务，由于没有类别信息，损失函数变成： max⁡θ∣ΠΔR(Z(θ),Π,ϵ)=R(Z,ϵ)\max_{\theta|\Pi} \Delta R(Z(\theta),\Pi,\epsilon)=R(Z, \epsilon) ，即：尽可能充分利用表征空间 。

Throught

  • 本文提出的方法从表征角度讲非常 make sense，但存在的问题是：依然无法摆脱 维度灾难，因此 MCR2MCR^2 也仅仅被用于低维度表征空间中，无法在神经网络的每一层都使用，在分类任务中也仅仅可以被当做一个在交叉熵的升级版本（交叉熵作用于类别维度，MCR2MCR^2 监督维度更高）。
  • 一个简单的想法确实可以有效提高聚类任务的模型效果，所以为后面的 Deep (Convolution) Networks from First Principles 提供了理论基础。

Posted on Edited on In Valine:

CUDA（Compute Unified Device Architecture，统一计算设备架构）资料：

GPU 体系结构

  • 物理模型
    image_1
    • 典型的 GPU 包含一组流处理器 (stream multi-processors, SM)，每个流处理器都有许多核心，硬件实现上这些核心之间可共享内存（shared memory）
  • 逻辑模型
    image_2
    • 逻辑模型中，引入了 Grid / Block / Thread 三级概念，逻辑模型与物理的对应关系如下：
      image_3

      因此：同一个 Block 中的 Thread 可共享 shared memory

  • Memory Hierarchy
    memory_hierarchy.png

    shared memory 速度几乎和 L1 cache 一样，比 local memory 和 global memory 都快的多（在物理上，local memory 和 global memory 是同一块 DRAM）

  • 在对 GPU 进行编程时，需要创建一组进程块 (thread blocks)，每个 thread 映射到单个核心，而 block 映射到流式多处理器 (SM)，如下图所示：
    cuda.jpg
  • 每个线程可由 threadIdx 和 blockIdx 索引，在实际应用中，可以有多维线程索引

共享内存优化

  • 以矩阵乘为例，A∈R1024×1024,B∈R1024×1024A\in \mathbb{R}^{1024\times 1024},B\in \mathbb{R}^{1024\times 1024}
    matmul.jpg
    • 同一个 block 中的多个 thread 可共享内存，因此可以重排同一个 block 中的 thread 数据，使得尽可能少的数据缓存到 shared memory 中
    • 优化前：
      • 每个 thread 需要计算输出矩阵中 8 * 8 的数据，需要从 local memory 中读取 8 * 8 * 1024 * 2 数据
      • 每个 block 中的 thread 之间没有数据共享，所以需要从 local memory 中读取 8∗8∗8∗8∗1024∗2=2238 * 8 * 8 * 8 * 1024 * 2 = 2^{23} 个矩阵元素
    • 优化后：
      • 每个 block 计算输出矩阵的 64 * 64 的数据最少需要 64∗1024∗2=21764 * 1024 * 2=2^{17} 的数据，可提前将这部分数据缓存到 shared memory
      • 然后每个 thread 从 shared memory 读数据计算，需读取 64∗1024∗2=21764 * 1024 * 2=2^{17} 个数据
    • 内存优化前后每个 block 读取数据对比：
      • 优化前：从 local memory 读取 2232^{23} 个矩阵元素
      • 优化后：从 local memory 读取 2172^{17} 个矩阵元素到 shared memory，再从 shared memory 读取 2172^{17} 个数据计算

Posted on Edited on In Valine:
  • TVM 是什么：是 Tensor Virtual Machine 的缩写，是一个 Open Deep Learning Compiler Stack（深度学习开源编译栈）
  • TVM 想干什么：将机器学习算法从开发阶段形态，通过变换和优化算法，使其变成部署形态
  • TVM 的原则：
    • 集成与最小化依赖
    • 利用硬件加速
    • 通用优化
  • TVM Module 层次结构：
    • IRModule：包含一个或多个 元张量函数 和一个 高层神经网络执行的抽象。通常用 @tvm.script.ir_module 装饰器装饰
    • tensorIR: 元张量函数。通常表示一个算子实例的计算过程，包含多个 计算块。通常用 @T.prim_func 装饰器装饰
    • 高层神经网络执行的抽象：IRModule 的程序入口。通常用 @R.function
    • block: 计算块。张量的基本计算单位，通常包含多个 计算轴 上的循环。通常用 with T.block(block_name) 来标明作用域
    • 计算轴：
      • 空间轴（spatial axis）：空间轴上循环的每个位置的计算独立于其他位置
      • 规约轴（reduce axis）：规约轴上的位置不会反映到最后的计算输出上
  • TVM Module 变换过程：
    • 自动程序优化
    • cuda 多线程优化
    • 内存优化
    • 图优化
    • 等等
  • TVM Module 执行过程： 
    1
    2
    3
    4
    5
    ex = relax.vm.build(MyModule, target="llvm")
    vm = relax.VirtualMachine(ex, tvm.cpu())
    nd_res = vm["main"](
        data_nd, nd_params["w0"], nd_params["b0"], nd_params["w1"], nd_params["b1"]
    )
    • 可执行程序 = build(IR_Module)
    • 虚拟机执行器 = 虚拟机(可执行程序)
    • 运行结果 = 虚拟机执行器(模型输入 + 模型权重)

Posted on Edited on In Valine:

URL

背景知识

GPU 体系结构

  • 物理模型
    cuda_hardware.png
    • 典型的 GPU 包含一组流处理器 (stream multi-processors, SM)，每个流处理器都有许多核心，硬件实现上这些核心之间可共享内存（shared memory）
  • 逻辑模型
    cuda.png
    • 逻辑模型中，引入了 Grid / Block / Thread 三级概念，逻辑模型与物理的对应关系如下图所示：
      cuda_map.png

      因此：同一个 Block 中的 Thread 可共享 shared memory

  • Memory Hierarchy
    memory_hierarchy.png

    shared memory 速度几乎和 L1 cache 一样，比 local memory 和 global memory 都快的多（在物理上，local memory 和 global memory 是同一块 DRAM）

  • 在对 GPU 进行编程时，需要创建一组进程块 (thread blocks)，每个 thread 映射到单个核心，而 block 映射到流式多处理器 (SM)，如下图所示：
    2.png
  • 每个线程可由 threadIdx 和 blockIdx 索引，在实际应用中，可以有多维线程索引

Element-wise Add GPU 加速

  • 两个向量 A 和 B，向量长度都为 1024,执行元素相加，并将结果存储在 C 中 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    @tvm.script.ir_module
    class MyModuleVecAdd:
        @T.prim_func
        def main(A: T.Buffer[(1024,), "float32"],
                B: T.Buffer[(1024,), "float32"],
                C: T.Buffer[(1024,), "float32"]) -> None:
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            for i in T.grid(1024):
                with T.block("C"):
                    vi = T.axis.remap("S", [i])
                    C[vi] = A[vi] + B[vi]
  • 首先将循环 i 拆分成两个循环: 
    1
    2
    3
    4
    sch = tvm.tir.Schedule(MyModuleVecAdd)
    block_C = sch.get_block("C")
    i, = sch.get_loops(block=block_C)
    i0, i1 = sch.split(i, [None, 128])
  • 将迭代器绑定到 GPU 线程块。 每个线程由两个索引进行表示 threadIdx.x 和 blockIdx.x 
    1
    2
    3
    sch.bind(i0, "blockIdx.x")
    sch.bind(i1, "threadIdx.x")
    sch.mod.show()
  • 绑定后的代码： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[1024, "float32"], B: T.Buffer[1024, "float32"], C: T.Buffer[1024, "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            for i_0 in T.thread_binding(8, thread="blockIdx.x"):
                for i_1 in T.thread_binding(128, thread="threadIdx.x"):
                    with T.block("C"):
                        vi = T.axis.spatial(1024, i_0 * 128 + i_1)
                        T.reads(A[vi], B[vi])
                        T.writes(C[vi])
                        C[vi] = A[vi] + B[vi]
  • 由于 Element-wise Add 不存在数据依赖，所以可以直接拆分到多个 block 中的多个 thread 中，一个 cycle 全部算完

窗口求和 GPU 加速

  • 相邻三个窗口求和，输入向量 A 长度 1026，输出 B 长度 1024。（即无 padding 的权重为 [1, 1, 1] 的 conv1d） 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    @tvm.script.ir_module
    class MyModuleWindowSum:
        @T.prim_func
        def main(A: T.Buffer[(1026,), "float32"],
                B: T.Buffer[(1024,), "float32"]) -> None:
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            for i in T.grid(1024):
                with T.block("C"):
                    vi = T.axis.remap("S", [i])
                    B[vi] = A[vi] + A[vi + 1] + A[vi + 2]
  • 拆分循环并绑定到 block 和 thread 
    1
    2
    3
    4
    5
    6
    7
    8
    sch = tvm.tir.Schedule(MyModuleWindowSum)
    nthread = 128
    block_C = sch.get_block("C")
    i,  = sch.get_loops(block=block_C)
    i0, i1 = sch.split(i, [None, nthread])
    sch.bind(i0, "blockIdx.x")
    sch.bind(i1, "threadIdx.x")
    sch.mod.show()
  • 拆分循环后 IRModule 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[1027, "float32"], B: T.Buffer[1024, "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            for i_0 in T.thread_binding(8, thread="blockIdx.x"):
                for i_1 in T.thread_binding(128, thread="threadIdx.x"):
                    # 启用 8 个 block 并发计算，每个 block 用 16 个 thread 并发
                    # 因此每一个 thread 只需要计算 1 次乘加
                    with T.block("C"):
                        vi = T.axis.spatial(1024, i_0 * 128 + i_1)
                        T.reads(A[vi : vi + 3])
                        T.writes(B[vi])
                        B[vi] = A[vi] + A[vi + 1] + A[vi + 2]
  • 提前缓存数据 
    1
    2
    3
    A_shared = sch.cache_read(block_C, read_buffer_index=0, storage_scope="shared")
    sch.compute_at(A_shared, i1)
    sch.mod.show()
  • 提前缓存数据后的 IRModule 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[1027, "float32"], B: T.Buffer[1024, "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            A_shared = T.alloc_buffer([1027], dtype="float32", scope="shared")
            for i_0 in T.thread_binding(8, thread="blockIdx.x"):
                for i_1 in T.thread_binding(128, thread="threadIdx.x"):
                    # 由上图 GPU 结构图可知
                    # 不同 block 无法共享 share memory
                    # 相同 block 的不同 thread 之间可以共享
                    # 所以输出 128 个结果需要 130 个输入（本行 128 个加下一行 2 个）
                    for ax0 in T.serial(130):
                        with T.block("A_shared"):
                            v0 = T.axis.spatial(1027, i_0 * 128 + ax0)
                            T.reads(A[v0])
                            T.writes(A_shared[v0])
                            A_shared[v0] = A[v0]
                    with T.block("C"):
                        vi = T.axis.spatial(1024, i_0 * 128 + i_1)
                        T.reads(A_shared[vi : vi + 3])
                        T.writes(B[vi])
                        B[vi] = A_shared[vi] + A_shared[vi + 1] + A_shared[vi + 2]
  • 缓存数据可以使用多线程优化
    • 因为内存是跨线程共享的，所以需要重新拆分循环并将获取过程的内部迭代器绑定到线程索引上，这种技术称为 cooperative fetching
    1
    2
    3
    4
    ax = sch.get_loops(A_shared)[-1]
    ax0, ax1 = sch.split(ax, [None, nthread])
    sch.bind(ax1, "threadIdx.x")
    sch.mod.show()
  • 缓存数据优化后 IRModule 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[1026, "float32"], B: T.Buffer[1024, "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            A_shared = T.alloc_buffer([1026], dtype="float32", scope="shared")
            for i_0 in T.thread_binding(8, thread="blockIdx.x"):
                for i_1 in T.thread_binding(128, thread="threadIdx.x"):
                    for ax0_0 in T.serial(2):
                        for ax0_1 in T.thread_binding(128, thread="threadIdx.x"):
                            with T.block("A_shared"):
                                # 由上图 GPU 结构图可知
                                # 不同 block 无法共享 share memory
                                # 相同 block 的不同 thread 之间可以共享
                                # 所以输出 128 个结果需要 130 个输入（本行 128 个加下一行 2 个）
                                v0 = T.axis.spatial(1026, i_0 * 128 + (ax0_0 * 128 + ax0_1))
                                T.where(ax0_0 * 128 + ax0_1 < 130)
                                T.reads(A[v0])
                                T.writes(A_shared[v0])
                                A_shared[v0] = A[v0]
                    with T.block("C"):
                        vi = T.axis.spatial(1024, i_0 * 128 + i_1)
                        T.reads(A_shared[vi : vi + 3])
                        T.writes(B[vi])
                        B[vi] = A_shared[vi] + A_shared[vi + 1] + A_shared[vi + 2]

矩阵乘法 GPU 加速

  • IRModule 基础实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    @tvm.script.ir_module
    class MyModuleMatmul:
        @T.prim_func
        def main(A: T.Buffer[(1024, 1024), "float32"],
                B: T.Buffer[(1024, 1024), "float32"],
                C: T.Buffer[(1024, 1024), "float32"]) -> None:
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            for i, j, k in T.grid(1024, 1024, 1024):
                with T.block("C"):
                    vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                    with T.init():
                        C[vi, vj] = 0.0
                    C[vi, vj] = C[vi, vj] + A[vi, vk] * B[vk, vj]
  • 绑定 block 和 thread + 本地存储分块优化
    3.png

    循环拆分，来增加整体内存复用，只需要从 A 和 B 加载一次条形数据（上图中的灰色部分），然后使用它们来计算矩阵乘法结果
    下面代码中设置 V = 8

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    def blocking(sch,
                tile_local_y,
                tile_local_x,
                tile_block_y,
                tile_block_x,
                tile_k):
        block_C = sch.get_block("C")
        C_local = sch.cache_write(block_C, 0, "local")
        i, j, k = sch.get_loops(block=block_C)
        i0, i1, i2 = sch.split(loop=i, factors=[None, tile_block_y, tile_local_y])
        j0, j1, j2 = sch.split(loop=j, factors=[None, tile_block_x, tile_local_x])
        k0, k1 = sch.split(loop=k, factors=[None, tile_k])
        sch.unroll(k1)
        sch.reorder(i0, j0, i1, j1, k0, k1, i2, j2)
        sch.reverse_compute_at(C_local, j1)
        sch.bind(i0, "blockIdx.y")
        sch.bind(j0, "blockIdx.x")
        sch.bind(i1, "threadIdx.y")
        sch.bind(j1, "threadIdx.x")
        sch.decompose_reduction(block_C, k0)
        return sch
    sch = tvm.tir.Schedule(MyModuleMatmul)
    sch = blocking(sch, 8, 8, 8, 8, 4)
    sch.mod.show()
  • 输出优化后的 IRModule 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[(1024, 1024), "float32"], B: T.Buffer[(1024, 1024), "float32"], C: T.Buffer[(1024, 1024), "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            C_local = T.alloc_buffer([1024, 1024], dtype="float32", scope="local")
            for i_0 in T.thread_binding(16, thread="blockIdx.y"):
                for j_0 in T.thread_binding(16, thread="blockIdx.x"):
                    for i_1 in T.thread_binding(8, thread="threadIdx.y"):
                        for j_1 in T.thread_binding(8, thread="threadIdx.x"):
                            # 一共使用 16 * 16 个 block 并发计算
                            # 每个 block 使用 8 * 8 个 thread 并发
                            # 所以每个 thread 只需计算输出为 8 * 8 的区域，因此只需要加载 A 中 8 行和 B 中 8 列数据
                            # 1. 初始化 8 * 8 的输出区域为 0
                            for i_2_init, j_2_init in T.grid(8, 8):
                                with T.block("C_init"):
                                    vi = T.axis.spatial(1024, i_0 * 64 + i_1 * 8 + i_2_init)
                                    vj = T.axis.spatial(1024, j_0 * 64 + j_1 * 8 + j_2_init)
                                    T.reads()
                                    T.writes(C_local[vi, vj])
                                    C_local[vi, vj] = T.float32(0)
                            
                            # 2. 计算 8 * 8 输出区域的值，共计算 8 * 8 * 1024 次乘加
                            for k_0 in T.serial(256):
                                for k_1 in T.unroll(4):
                                    for i_2, j_2 in T.grid(8, 8):
                                        with T.block("C_update"):
                                            vi = T.axis.spatial(1024, i_0 * 64 + i_1 * 8 + i_2)
                                            vj = T.axis.spatial(1024, j_0 * 64 + j_1 * 8 + j_2)
                                            vk = T.axis.reduce(1024, k_0 * 4 + k_1)
                                            T.reads(C_local[vi, vj], A[vi, vk], B[vk, vj])
                                            T.writes(C_local[vi, vj])
                                            C_local[vi, vj] = C_local[vi, vj] + A[vi, vk] * B[vk, vj]
                            
                            # 3. 把每个 thread 的 8 * 8 的输出区域拼成最后的 1024 * 1024 的输出
                            for ax0, ax1 in T.grid(8, 8):
                                with T.block("C_local"):
                                    v0 = T.axis.spatial(1024, i_0 * 64 + i_1 * 8 + ax0)
                                    v1 = T.axis.spatial(1024, j_0 * 64 + j_1 * 8 + ax1)
                                    T.reads(C_local[v0, v1])
                                    T.writes(C[v0, v1])
                                    C[v0, v1] = C_local[v0, v1]
  • 共享内存优化
    4.png

    与上图不同，图中矩阵 C 中 L * L 灰色区域表示一个 block 的计算输出
    每个 L * L 灰色区域由多个 V * V 的小区域组成，表示一个 thread 的输出

    • 同一个 block 中的多个 thread 可共享内存，因此可以重排同一个 block 中的 thread 数据，使得尽可能少的数据缓存到 shared memory 中

    • 优化前：

      • 每个 thread 需要计算输出矩阵中 8 * 8 的数据，需要从 local memory 中读取 8 * 8 * 1024 * 2 数据
      • 每个 block 中的 thread 之间没有数据共享，所以需要从 local memory 中读取 8∗8∗8∗8∗1024∗2=2238 * 8 * 8 * 8 * 1024 * 2 = 2^{23} 个矩阵元素

    • 优化后：

      • 每个 block 计算输出矩阵的 64 * 64 的数据最少需要 64∗1024∗2=21764 * 1024 * 2=2^{17} 的数据，可提前将这部分数据缓存到 shared memory
      • 然后每个 thread 从 shared memory 读数据计算，需读取 64∗1024∗2=21764 * 1024 * 2=2^{17} 个数据

    • 内存优化前后每个 block 读取数据对比：

      • 优化前：从 local memory 读取 2232^{23} 个矩阵元素
      • 优化后：从 local memory 读取 2172^{17} 个矩阵元素到 shared memory，再从 shared memory 读取 2172^{17} 个数据计算

    • 优化过程：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    def cache_read_and_coop_fetch(sch, block, nthread, read_idx, read_loc):
        read_cache = sch.cache_read(block=block, read_buffer_index=read_idx, storage_scope="shared")
        sch.compute_at(block=read_cache, loop=read_loc)
        # vectorized cooperative fetch
        inner0, inner1 = sch.get_loops(block=read_cache)[-2:]
        inner = sch.fuse(inner0, inner1)
        _, tx, vec = sch.split(loop=inner, factors=[None, nthread, 4])
        sch.vectorize(vec)
        sch.bind(tx, "threadIdx.x")
    def blocking_with_shared(
        sch,
        tile_local_y,
        tile_local_x,
        tile_block_y,
        tile_block_x,
        tile_k):
        block_C = sch.get_block("C")
        C_local = sch.cache_write(block_C, 0, "local")
        i, j, k = sch.get_loops(block=block_C)
        i0, i1, i2 = sch.split(loop=i, factors=[None, tile_block_y, tile_local_y])
        j0, j1, j2 = sch.split(loop=j, factors=[None, tile_block_x, tile_local_x])
        k0, k1 = sch.split(loop=k, factors=[None, tile_k])
        sch.reorder(i0, j0, i1, j1, k0, k1, i2, j2)
        sch.reverse_compute_at(C_local, j1)
        sch.bind(i0, "blockIdx.y")
        sch.bind(j0, "blockIdx.x")
        tx = sch.fuse(i1, j1)
        sch.bind(tx, "threadIdx.x")
        nthread = tile_block_y * tile_block_x
        cache_read_and_coop_fetch(sch, block_C, nthread, 0, k0)
        cache_read_and_coop_fetch(sch, block_C, nthread, 1, k0)
        sch.decompose_reduction(block_C, k0)
        return sch
    sch = tvm.tir.Schedule(MyModuleMatmul)
    sch = blocking_with_shared(sch, 8, 8, 8, 8, 8)
    sch.mod.show()
    • 优化后 IRModule
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    @tvm.script.ir_module
    class Module:
        @T.prim_func
        def main(A: T.Buffer[(1024, 1024), "float32"], B: T.Buffer[(1024, 1024), "float32"], C: T.Buffer[(1024, 1024), "float32"]) -> None:
            # function attr dict
            T.func_attr({"global_symbol": "main", "tir.noalias": True})
            # body
            # with T.block("root")
            C_local = T.alloc_buffer([1024, 1024], dtype="float32", scope="local")
            A_shared = T.alloc_buffer([1024, 1024], dtype="float32", scope="shared")
            B_shared = T.alloc_buffer([1024, 1024], dtype="float32", scope="shared")
            for i_0 in T.thread_binding(16, thread="blockIdx.y"):
                for j_0 in T.thread_binding(16, thread="blockIdx.x"):
                    for i_1_j_1_fused in T.thread_binding(64, thread="threadIdx.x"):
                        for i_2_init, j_2_init in T.grid(8, 8):
                            with T.block("C_init"):
                                vi = T.axis.spatial(1024, i_0 * 64 + i_1_j_1_fused // 8 * 8 + i_2_init)
                                vj = T.axis.spatial(1024, j_0 * 64 + i_1_j_1_fused % 8 * 8 + j_2_init)
                                T.reads()
                                T.writes(C_local[vi, vj])
                                C_local[vi, vj] = T.float32(0)
                        for k_0 in T.serial(128):
                            for ax0_ax1_fused_0 in T.serial(2):
                                for ax0_ax1_fused_1 in T.thread_binding(64, thread="threadIdx.x"):
                                    for ax0_ax1_fused_2 in T.vectorized(4):
                                        with T.block("A_shared"):
                                            v0 = T.axis.spatial(1024, i_0 * 64 + (ax0_ax1_fused_0 * 256 + ax0_ax1_fused_1 * 4 + ax0_ax1_fused_2) // 8)
                                            v1 = T.axis.spatial(1024, k_0 * 8 + (ax0_ax1_fused_0 * 256 + ax0_ax1_fused_1 * 4 + ax0_ax1_fused_2) % 8)
                                            T.reads(A[v0, v1])
                                            T.writes(A_shared[v0, v1])
                                            A_shared[v0, v1] = A[v0, v1]
                            for ax0_ax1_fused_0 in T.serial(2):
                                for ax0_ax1_fused_1 in T.thread_binding(64, thread="threadIdx.x"):
                                    for ax0_ax1_fused_2 in T.vectorized(4):
                                        with T.block("B_shared"):
                                            v0 = T.axis.spatial(1024, k_0 * 8 + (ax0_ax1_fused_0 * 256 + ax0_ax1_fused_1 * 4 + ax0_ax1_fused_2) // 64)
                                            v1 = T.axis.spatial(1024, j_0 * 64 + (ax0_ax1_fused_0 * 256 + ax0_ax1_fused_1 * 4 + ax0_ax1_fused_2) % 64)
                                            T.reads(B[v0, v1])
                                            T.writes(B_shared[v0, v1])
                                            B_shared[v0, v1] = B[v0, v1]
                            for k_1, i_2, j_2 in T.grid(8, 8, 8):
                                with T.block("C_update"):
                                    vi = T.axis.spatial(1024, i_0 * 64 + i_1_j_1_fused // 8 * 8 + i_2)
                                    vj = T.axis.spatial(1024, j_0 * 64 + i_1_j_1_fused % 8 * 8 + j_2)
                                    vk = T.axis.reduce(1024, k_0 * 8 + k_1)
                                    T.reads(C_local[vi, vj], A_shared[vi, vk], B_shared[vk, vj])
                                    T.writes(C_local[vi, vj])
                                    C_local[vi, vj] = C_local[vi, vj] + A_shared[vi, vk] * B_shared[vk, vj]
                        for ax0, ax1 in T.grid(8, 8):
                            with T.block("C_local"):
                                v0 = T.axis.spatial(1024, i_0 * 64 + i_1_j_1_fused // 8 * 8 + ax0)
                                v1 = T.axis.spatial(1024, j_0 * 64 + i_1_j_1_fused % 8 * 8 + ax1)
                                T.reads(C_local[v0, v1])
                                T.writes(C[v0, v1])
                                C[v0, v1] = C_local[v0, v1]

程序自动变换

1
2
3
4
5
6
7
8
9
10
11
12
from tvm import meta_schedule as ms
sch_tuned = ms.tune_tir(
    mod=MyModuleMatmul,
    target="nvidia/tesla-p100",
    config=ms.TuneConfig(
      max_trials_global=64,
      num_trials_per_iter=64,
    ),
    work_dir="./tune_tmp",
    task_name="main"
)
sch_tuned.mod.show()

Posted on Edited on In Valine:

URL

使用 Builder 创建 IRModule

从张量表达式创建 TensorIR（主张量函数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from tvm import te
# 定义 TensorIR 输入
A = te.placeholder((128, 128), name="A", dtype="float32")
B = te.placeholder((128, 128), name="B", dtype="float32")
type(A)
# tvm.te.tensor.Tensor
A.shape
# [128, 128]
# 由张量表达式自动生成 TensorIR
def te_matmul(A: te.Tensor, B: te.Tensor) -> te.Tensor:
    assert A.shape[1] == B.shape[0]
    n = A.shape[0]
    m = B.shape[1]
    k = te.reduce_axis((0, A.shape[1]), name="k")
    # 由张量表达式自动生成 TensorIR
    # 调用格式是：te.compute(output_shape, lambda, TensorIR_name)
    return te.compute(
        (n, m), lambda i, j: te.sum(A[i, k] * B[k, j], axis=k), name="matmul"
    )
C = te_matmul(A, B)
# 打印自动生成的 TensorIR，函数输入即为 [A, B, C]
te.create_prim_func([A, B, C]).show()
  • 输出（自动生成的主张量函数）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# from tvm.script import tir as T
@T.prim_func
def func(
    A: T.Buffer[(128, 128), "float32"],
    B: T.Buffer[(128, 128), "float32"],
    matmul: T.Buffer[(128, 128), "float32"],
) -> None:
    # function attr dict
    T.func_attr({"global_symbol": "main", "tir.noalias": True})
    # body
    # with T.block("root")
    for i0, i1, i2 in T.grid(128, 128, 128):
        with T.block("matmul"):
            i, j, k = T.axis.remap("SSR", [i0, i1, i2])
            T.reads(A[i, k], B[k, j])
            T.writes(matmul[i, j])
            with T.init():
                matmul[i, j] = T.float32(0)
            matmul[i, j] = matmul[i, j] + A[i, k] * B[k, j]

使用 BlockBuilder 构造 IRModule

  • 自动生成的主张量函数还需要 计算图抽象 来将计算图拼起来
1
2
3
4
5
6
7
8
9
10
11
12
A = relax.Var("A", (128, 128), relax.DynTensorType(2, "float32"))
B = relax.Var("B", (128, 128), relax.DynTensorType(2, "float32"))
# 使用 BlockBuilder 将多个张量函数拼接成一个 IRModule
bb = relax.BlockBuilder()
with bb.function("main"):
    with bb.dataflow():
        C = bb.emit_te(te_matmul, A, B)
        D = bb.emit_te(te_relu, C)
        R = bb.emit_output(D)
    bb.emit_func_output(R, params=[A, B])
MyModule = bb.get()
MyModule.show()
  • 输出（IRModule）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tvm.script.ir_module
class Module:
    @T.prim_func
    def te_matmul(rxplaceholder: T.Buffer[(128, 128), "float32"], rxplaceholder_1: T.Buffer[(128, 128), "float32"], matmul: T.Buffer[(128, 128), "float32"]) -> None:
        ...
    @T.prim_func
    def te_relu(rxplaceholder: T.Buffer[(128, 128), "float32"], relu: T.Buffer[(128, 128), "float32"]) -> None:
        ...
    @R.function
    def main(A: Tensor((128, 128), "float32"), B: Tensor((128, 128), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv = R.call_tir(te_matmul, (A, B), (128, 128), dtype="float32")
            lv1 = R.call_tir(te_relu, (lv,), (128, 128), dtype="float32")
            gv: Tensor((128, 128), "float32") = lv1
            R.output(gv)
        return gv
  • 使用 BlockBuilder 创建 IRModule 与直接创建 IRMoudle 的对比
    integration_block_builder.png
  • bb.emit_te 做了以下事情：
    • 为 A 和 B 创建一个输入 te.placeholder
    • 通过 te_matmul 函数运行它们
    • 调用 te.create_prim_func 来创建一个 TensorIR 函数
    • 通过 call_tir 生成对函数的调用

从 Pytorch 映射到 IRModule

Pytorch 模型

1
2
3
4
5
6
7
8
9
10
11
class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()
        self.weight = nn.Parameter(torch.randn(128, 128))
    def forward(self, x):
        x = torch.matmul(x, self.weight)
        x = torch.relu(x)
        return x
model = MyModel()
# 生成 Pytorch 计算图
fx_module = fx.symbolic_trace(model)

构造计算图之间的映射变换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# pytorch module parameter to IRModule parameter
def map_param(param: nn.Parameter):
    ndim = len(param.data.shape)
    return relax.const(
        param.data.cpu().numpy(), relax.DynTensorType(ndim, "float32")
    )
# pytorch module attribute to IRModule attribute
def fetch_attr(fx_mod, target: str):
    """Helper function to fetch an attr"""
    target_atoms = target.split('.')
    attr_itr = fx_mod
    for i, atom in enumerate(target_atoms):
        if not hasattr(attr_itr, atom):
            raise RuntimeError(f"Node referenced nonexistant target {'.'.join(target_atoms[:i])}")
        attr_itr = getattr(attr_itr, atom)
    return attr_itr
def from_fx(fx_mod, input_shapes, call_function_map, call_module_map):
    input_index = 0
    node_map = {}
    named_modules = dict(fx_mod.named_modules())
    bb = relax.BlockBuilder()
    fn_inputs = []
    fn_output = None
    with bb.function("main"):
        with bb.dataflow():
            for node in fx_mod.graph.nodes:
                if node.op == "placeholder":
                    # create input placeholder
                    shape = input_shapes[input_index]
                    input_index += 1
                    input_var = relax.Var(
                        node.target, shape, relax.DynTensorType(len(shape), "float32")
                    )
                    fn_inputs.append(input_var)
                    node_map[node] = input_var
                elif node.op == "get_attr":
                    node_map[node] = map_param(fetch_attr(fx_mod, node.target))
                elif node.op == "call_function":
                    node_map[node] = call_function_map[node.target](bb, node_map, node)
                elif node.op == "call_module":
                    named_module = named_modules[node.target]
                    node_map[node] = call_module_map[type(named_module)](bb, node_map, node, named_module)
                elif node.op == "output":
                    output = node_map[node.args[0]]
                    assert fn_output is None
                    fn_output = bb.emit_output(output)
        # output and finalize the function
        bb.emit_func_output(output, fn_inputs)
    return bb.get()

映射 Pytorch Module 到 TensorIR

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# TensorIR 映射变换
def map_matmul(bb, node_map, node: fx.Node):
    A = node_map[node.args[0]]
    B = node_map[node.args[1]]
    return bb.emit_te(te_matmul, A, B)
# TensorIR 映射变换
def map_relu(bb, node_map, node: fx.Node):
    A = node_map[node.args[0]]
    return bb.emit_te(te_relu, A)
MyModule = from_fx(
    fx_module,
    input_shapes = [(1, 128)],
    call_function_map = {
      torch.matmul: map_matmul,
      torch.relu: map_relu,
    },
    call_module_map={},
)
MyModule.show()
  • 映射后的 IRModule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
@tvm.script.ir_module
class Module:
    @T.prim_func
    def te_matmul(rxplaceholder: T.Buffer[(1, 128), "float32"], rxplaceholder_1: T.Buffer[(128, 128), "float32"], matmul: T.Buffer[(1, 128), "float32"]) -> None:
        ...
    @T.prim_func
    def te_relu(rxplaceholder: T.Buffer[(1, 128), "float32"], relu: T.Buffer[(1, 128), "float32"]) -> None:
        ...
    @R.function
    def main(x: Tensor((1, 128), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv = R.call_tir(te_matmul, (x, meta[relay.Constant][0]), (1, 128), dtype="float32")
            lv1 = R.call_tir(te_relu, (lv,), (1, 128), dtype="float32")
            gv: Tensor((1, 128), "float32") = lv1
            R.output(gv)
        return lv1

或映射到 Pytorch Module 到 IRModule 更高层的算子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def map_nn_relu_op(bb, node_map, node, nn_mod):
    A = node_map[node.args[0]]
    return bb.emit(relax.op.relu(A))
def map_nn_linear_op(bb, node_map, node, nn_mod):
    x = node_map[node.args[0]]
    w = map_param(nn_mod.weight)
    if nn_mod.bias is not None:
        b = map_param(nn_mod.bias)
    y = bb.emit(relax.op.dense(x, w))
    return bb.emit(relax.op.add(y, b))
MLPModuleHighLevel = from_fx(
    fx.symbolic_trace(mlp_model),
    input_shapes = [(1, 784)],
    call_function_map={
    },
    call_module_map={
        torch.nn.Linear: map_nn_linear_op,
        torch.nn.ReLU: map_nn_relu_op,
    },
)
MLPModuleHighLevel.show()
  • 输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
@tvm.script.ir_module
class Module:
    @R.function
    def main(x: Tensor((1, 784), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv: Tensor((1, 128), "float32") = relax.nn.dense(x, meta[relay.Constant][0])
            lv1: Tensor((1, 128), "float32") = relax.add(lv, meta[relay.Constant][1])
            lv2: Tensor((1, 128), "float32") = relax.nn.relu(lv1)
            lv3: Tensor((1, 10), "float32") = relax.nn.dense(lv2, meta[relay.Constant][2])
            lv4: Tensor((1, 10), "float32") = relax.add(lv3, meta[relay.Constant][3])
            gv: Tensor((1, 10), "float32") = lv4
            R.output(gv)
        return lv4

总结

  • 张量表达式 API 允许我们创建原始的 TensorIR 函数
  • BlockBuilder API 通过 emit_te 和其他函数创建 IRModule
  • 通过将模型转换为 IRModule，实现与现有的机器学习框架的整合

Posted on Edited on In Valine:

URL

自动程序优化的原因

  • MLC 的本质是张量函数之间的转换，但我们不知道哪种转换是让模型运行更快的，所以需要使用自动程序优化，去自动搜索最有转换。

自动程序优化过程

end-to-end 构建模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# IR_Module 使用自定义主张量函数和库张量函数
@tvm.script.ir_module
class MyModuleMixture:
    @T.prim_func
    def linear0(
        X: T.Buffer[(1, 784), "float32"],
        W: T.Buffer[(128, 784), "float32"],
        B: T.Buffer[(128,), "float32"],
        Z: T.Buffer[(1, 128), "float32"],
    ):
        T.func_attr({"global_symbol": "linear0", "tir.noalias": True})
        ...
    @R.function
    def main(
        x: Tensor((1, 784), "float32"),
        w0: Tensor((128, 784), "float32"),
        b0: Tensor((128,), "float32"),
        w1: Tensor((10, 128), "float32"),
        b1: Tensor((10,), "float32"),
    ):
        with R.dataflow():
            lv0 = R.call_tir(linear0, (x, w0, b0), (1, 128), dtype="float32")
            lv1 = R.call_tir("env.relu", (lv0,), (1, 128), dtype="float32")
            out = R.call_tir("env.linear", (lv1, w1, b1), (1, 10), dtype="float32")
            R.output(out)
        return out
# 注册库张量函数
@tvm.register_func("env.linear", override=True)
def torch_linear(
    x: tvm.nd.NDArray, w: tvm.nd.NDArray, b: tvm.nd.NDArray, out: tvm.nd.NDArray
):
    ...
# 注册库张量函数
@tvm.register_func("env.relu", override=True)
def lnumpy_relu(x: tvm.nd.NDArray, out: tvm.nd.NDArray):
    ...
# 绑定模型权重参数（nd_params 是模型权重），作用类似于 functools.partial()
MyModuleWithParams = relax.transform.BindParams("main", nd_params)(MyModuleMixture)
# IR_Module -> 可执行程序 -> 虚拟机执行器
ex = relax.vm.build(MyModuleWithParams, target="llvm")
vm = relax.VirtualMachine(ex, tvm.cpu())
# 执行
nd_res = vm["main"](data_nd)
# 测速
ftimer = vm.module.time_evaluator("main", tvm.cpu(), number=100)

自动优化 linear0 主张量函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 调优 API 只接受一个带有一个 main 函数的 IRModule，所以需要将原始 IRModule 中的 linear0 转成新 IRModule 的 main 函数
mod_linear = tvm.IRModule.from_expr(MyModuleMixture["linear0"].with_attr("global_symbol", "main"))
# 打印新IRModule
IPython.display.HTML(code2html(mod_linear.script()))
# 打印输出
@tvm.script.ir_module
class Module:
    @T.prim_func
    def main(
        X: T.Buffer[(1, 784), "float32"],
        W: T.Buffer[(128, 784), "float32"],
        B: T.Buffer[(128,), "float32"],
        Z: T.Buffer[(1, 128), "float32"],
    ):
        # 函数中内容是 MyModuleMixture.linear0
# 自动调优 API，input 是需要调优的 IRModule，output 是调优后的 schedule，schedule.mod 是调优后的 IRModule
sch_tuned_linear = ms.tune_tir(
    mod=mod_linear,                 # 待调优 IRModule
    target="llvm --num-cores=1",    # 调优目标
    config=ms.TuneConfig(           # 自动调优配置
      max_trials_global=64,
      num_trials_per_iter=64,
    ),
    work_dir="./tune_tmp",
    task_name="main",
)
# 将返回的 IRModule 中的 main 函数更新到原 IRModule 的 linear0 中
# 绑定参数
MyModuleWithParams2 = relax.transform.BindParams("main", nd_params)(MyModuleMixture)
# 获取调优后的 main 函数
new_func = sch_tuned_linear.mod["main"].with_attr("global_symbol", "linear0")
# 获取原 IRModule 的 linear0 张量函数
gv = MyModuleWithParams2.get_global_var("linear0")
# 更新调优后的 main 函数到原 IRModule 的 linear0 张量函数
MyModuleWithParams2.update_func(gv, new_func)
# 重新测速，速度变快

Posted on Edited on In Valine:

URL

机器学习编译的本质与关注点

  • MLC 的本质：张量函数之间的转换
  • MLC 的关注点：
    • 所以可能的张量函数抽象表达
    • 所有可能的张量函数转换

构造 IR_Module

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
@tvm.script.ir_module
class MyModule:
    @T.prim_func
    def relu0(X: T.Buffer[(1, 128), "float32"], Y: T.Buffer[(1, 128), "float32"]):
        # function attr dict
        T.func_attr({"global_symbol": "relu0", "tir.noalias": True})
        for i, j in T.grid(1, 128):
            with T.block("Y"):
                vi, vj = T.axis.remap("SS", [i, j])
                Y[vi, vj] = T.max(X[vi, vj], T.float32(0))
    @T.prim_func
    def linear0(
        X: T.Buffer[(1, 784), "float32"],
        W: T.Buffer[(128, 784), "float32"],
        B: T.Buffer[(128,), "float32"],
        Z: T.Buffer[(1, 128), "float32"],
    ):
        T.func_attr({"global_symbol": "linear0", "tir.noalias": True})
        Y = T.alloc_buffer((1, 128), "float32")
        for i, j, k in T.grid(1, 128, 784):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
        for i, j in T.grid(1, 128):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                Z[vi, vj] = Y[vi, vj] + B[vj]
    @T.prim_func
    def linear1(
        X: T.Buffer[(1, 128), "float32"],
        W: T.Buffer[(10, 128), "float32"],
        B: T.Buffer[(10,), "float32"],
        Z: T.Buffer[(1, 10), "float32"],
    ):
        T.func_attr({"global_symbol": "linear1", "tir.noalias": True})
        Y = T.alloc_buffer((1, 10), "float32")
        for i, j, k in T.grid(1, 10, 128):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
        for i, j in T.grid(1, 10):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                Z[vi, vj] = Y[vi, vj] + B[vj]
    @R.function
    def main(
        x: Tensor((1, 784), "float32"),
        w0: Tensor((128, 784), "float32"),
        b0: Tensor((128,), "float32"),
        w1: Tensor((10, 128), "float32"),
        b1: Tensor((10,), "float32"),
    ):
        with R.dataflow():
            lv0 = R.call_tir(linear0, (x, w0, b0), (1, 128), dtype="float32")
            lv1 = R.call_tir(relu0, (lv0,), (1, 128), dtype="float32")
            out = R.call_tir(linear1, (lv1, w1, b1), (1, 10), dtype="float32")
            R.output(out)
        return out
  • @tvm.script.ir_module 装饰 IR_Module
  • @T.prim_func 装饰 主张量函数
  • @R.function 装饰 高层神经网络执行的抽象，（将整个 IR_Module 中的主张量函数串起来组成一个计算图）
  • R.dataflow() 用于标记程序计算图区域
  • R.call_tir(prim_func, inputs, output_shape, dtype) 分配输出内存并和输入一起输入主张量函数

构建并运行模型

1
2
3
4
5
ex = relax.vm.build(MyModule, target="llvm")
vm = relax.VirtualMachine(ex, tvm.cpu())
nd_res = vm["main"](
    data_nd, nd_params["w0"], nd_params["b0"], nd_params["w1"], nd_params["b1"]
)
  • 可执行文件 = build(IR_Module)
  • 虚拟机执行器 = 虚拟机(可执行文件)
  • 运行结果 = 虚拟机执行器(模型输入)

使用现有库避免重复造轮子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
@tvm.script.ir_module
class MyModuleWithExternCall:
    @R.function
    def main(
        x: Tensor((1, 784), "float32"),
        w0: Tensor((128, 784), "float32"),
        b0: Tensor((128,), "float32"),
        w1: Tensor((10, 128), "float32"),
        b1: Tensor((10,), "float32"),
    ):
        # block 0
        with R.dataflow():
            lv0 = R.call_tir("env.linear", (x, w0, b0), (1, 128), dtype="float32")
            lv1 = R.call_tir("env.relu", (lv0,), (1, 128), dtype="float32")
            out = R.call_tir("env.linear", (lv1, w1, b1), (1, 10), dtype="float32")
            R.output(out)
        return out
  • 上图中的 env.linear 是库张量函数，同一个 IR_Module 中可使用库张量函数，也可使用自定义张量函数，也可以二者混用。
1
2
3
@tvm.register_func("env.linear", override=True)
def torch_linear(x: tvm.nd.NDArray, w: tvm.nd.NDArray, b: tvm.nd.NDArray, out: tvm.nd.NDArray):
    ...
  • @tvm.register_func，注册库张量函数

绑定参数到 IR_Module

  • 以上的所有 IR_Module 都是在调用时才传入 数据 和 权重参数，但 权重参数 是不变的，所以可以将 权重参数 提前绑定到 IR_Module 中，调用时只传入输入数据。
1
MyModuleWithParams = relax.transform.BindParams("main", nd_params)(MyModuleMixture)
  • relax.transform.BindParams(计算图入口函数，模型参数)(IR_Module) 将模型参数绑定到 IR_Module 的计算图入口函数中，返回一个绑定好模型参数的 IR_Module。

总结

  • 计算图抽象（一般表示 main 函数） 有助于将元张量函数拼接在一起以进行端到端执行。
  • Relax 抽象的关键要素包括
    • call_tir 构造，将目标传递规范的元函数嵌入到计算图中
    • Dataflow block
  • 计算图允许调用环境库函数和 TensorIR 函数。

Posted on Edited on In Valine:

三种成像相关坐标系

  • 像素坐标系：一种 2D 坐标，以图片左上角为原点，横轴（宽度方向）向右为 x 轴正方向，纵轴（高度方向）向下为 y 轴正方向，单位是像素
  • 相机坐标系：一种 3D 坐标，以相机光心为原点，垂直相机平面远离相机方向为 z 轴正方向，垂直于 z 轴且平行于相机平面，水平向右为 x 轴正方向，竖直向下为 y 轴正方向，单位是米
  • 世界坐标系：一种 3D 坐标，一种人为定义的，且x, y, z 轴两两垂直的坐标系，单位是米

相机内参

  • 相机内参可以实现像素坐标系与相机坐标系之间相互转换，通常使用一个 3 * 3 矩阵表示
    camera_1.jpg
    camera_2.jpg

  • 根据小孔成像和相似三角形原理，可以得出相机坐标系与成像坐标系点的对应关系：Zf=Xx=Yy\frac{Z}{f}=\frac{X}{x}=\frac{Y}{y}
    其中：(X,Y,Z)(X,Y,Z) 为相机坐标系下的点的坐标， (x,y)(x, y) 为投影到成像平面上的点的坐标， ff 表示焦距。

  • 再根据成像坐标系到像素坐标系的对应关系：

    u=α⋅x+cxv=β⋅y+cy\begin{matrix} u=\alpha \cdot x + c_x \\ v = \beta \cdot y + c_y \end{matrix}

    其中：

    • α,β\alpha,\beta 分别表示 x,yx, y 方向上成像宽度到像素宽度的投影
    • 由于成像坐标系原点为成像中心，像素坐标系原点为像素左上角，所以需要加上原点的偏移， cx,cyc_x,c_y 分别表示 x,yx, y 方向上原点的偏移。

  • 所以，相机坐标系 (X,Y,Z)(X,Y,Z) 与像素坐标系 (u,v)(u, v) 可通过相机内参相互转换：

    Z[uv1]=[fx0cx0fycy001][XYZ]Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}X\\ Y\\ Z \end{bmatrix}

    其中： fx=α⋅f, fy=β⋅f, Zf_x=\alpha \cdot f,\ f_y=\beta \cdot f,\ Z 表示相机坐标系下的深度

  • [fx0cx0fycy001]\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} 被称为相机内参 KK

相机外参

  • 相机外参可以实现相机坐标系与世界坐标系之间相互转换（刚体变换），通常用一个 3 * 3 的旋转矩阵 RR 和一个 3 * 1 的平移矩阵 TT 表示：

    [XcYcZc]=[R11R12R13R21R22R23R31R32R33][XwYwZw]+[T1T2T3]\begin{bmatrix} X_c\\ Y_c \\ Z_c \end{bmatrix}=\begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} X_w\\ Y_w \\ Z_w \end{bmatrix} + \begin{bmatrix} T_{1} \\ T_{2} \\ T_{3} \end{bmatrix}

    其中： (Xc,Yc,Zc)(X_c,Y_c,Z_c) 表示相机坐标系下的点， (Xw,Yw,Zw)(X_w,Y_w,Z_w) 表示世界坐标系下的点

  • 齐次化之后，得到一个 4 * 4 的矩阵：

    [XcYcZc1]=[R11R12R13T1R21R22R23T2R31R32R33T30001][XwYwZw1]\begin{bmatrix} X_c\\ Y_c \\ Z_c \\ 1\end{bmatrix}=\begin{bmatrix} R_{11} & R_{12} & R_{13} & T_1 \\ R_{21} & R_{22} & R_{23} & T_2 \\ R_{31} & R_{32} & R_{33} & T_3 \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} X_w\\ Y_w \\ Z_w \\ 1\end{bmatrix}

总结

  • camera intrisic matrix×camera coordinate system=depth in camera coordinatesystem⋅image coordinate systemcamera\ intrisic\ matrix \times camera\ coordinate\ system = depth\ in\ camera\ coordinate system \cdot image\ coordinate\ system
  • camera extrisic matrix×world coordinate system=camera coordinate systemcamera\ extrisic\ matrix \times world\ coordinate\ system = camera\ coordinate\ system
  • camera intrisic matrix×camera extrisic matrix×world coordinate system=depth in camera coordinatesystem⋅image coordinate systemcamera\ intrisic\ matrix \times camera\ extrisic\ matrix \times world\ coordinate\ system = depth\ in\ camera\ coordinate system \cdot image\ coordinate\ system